题目内容
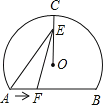
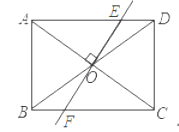
【题目】如图,在矩形ABCD中,AB=4,BC=6,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是( )
A.1B.![]() C.2D.
C.2D.![]()
【答案】D
【解析】
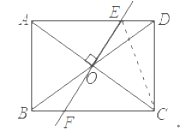
连接CE,由矩形的性质得出∠ADC=90°,CD=AB=4,AD=BC=6,OA=OC,由线段垂直平分线的性质得出AE=CE,设DE=x,则CE=AE=6x,在Rt△CDE中,由勾股定理得出方程,解方程即可.
连接CE,如图所示:
∵四边形ABCD是矩形,
∴∠ADC=90°,CD=AB=4,AD=BC=6,OA=OC,
∵EF⊥AC,
∴AE=CE,
设DE=x,则CE=AE=6﹣x,
在Rt△CDE中,由勾股定理得:x2+42=(6﹣x)2,
解得:x=![]() ,
,
即DE=![]() ;
;
故选:D.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
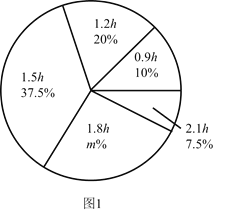
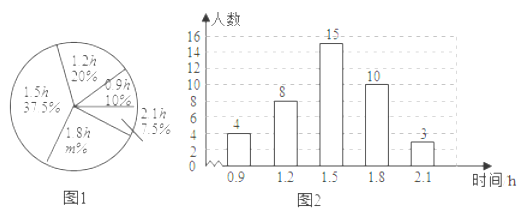
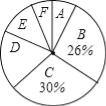
阳光同学一线名师全优好卷系列答案【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>4.0 | 3 |
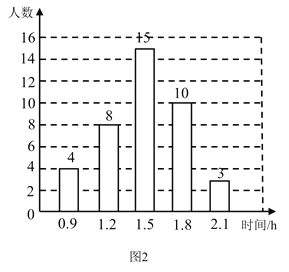
根据以上信息,解答下列问题
(1)家庭用水量在4.0<x≤6.5范围内的家庭有 户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为 户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在 组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一段时间后,记录下这种植物高度的增长情况(如下表):
温度x/℃ | … | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
植物每天高度的增长量y/mm | … | 41 | 49 | 49 | 41 | 25 | 1 | … |
由这些数据,科学家推测出植物每天高度的增长量y是温度x的二次函数,那么下列三个结论:
①该植物在0℃时,每天高度的增长量最大;
②该植物在﹣6℃时,每天高度的增长量能保持在25mm左右;
③该植物与大多数植物不同,6℃以上的环境下高度几乎不增长.
上述结论中,所有正确结论的序号是
A. ①②③ B. ①③ C. ①② D. ②③