题目内容
【题目】在“六城”同创活动中,为努力把我市建成“国家园林城市”,绿化公司计划购买A,B,C三种绿化树共800株,用20辆货车一次运回,对我市城区新建道路进行绿化.按计划,20辆货车都要装运,每辆货车只能装运同一种绿化树,且必须装满.根据下表提供的信息,解答以下问题:
绿 化 树 品 种 | A | B | C |
每辆货车运载量(株) | 40 | 48 | 32 |
每株树苗的价格(元) | 20 | 50 | 30 |
(1)设装运A种绿化树的车辆数为x,装运B种绿化树的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种绿化树的车辆数都不多于8辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若在“六城”同创活动中要求“厉行节约”办实事,则应采用(2)中的哪种安排方案?为什么?
【答案】
(1)解:由题意可知:装运C种绿化树的车辆数为(20﹣x﹣y),
据题意可列如下方程:40x+48y+32(20﹣x﹣y)=800,
解得:y=﹣ ![]() x+10,
x+10,
故y与x之间的函数关系式为:y=﹣ ![]() x+10
x+10
(2)解:由题意可得如下不等式组:
 ,即
,即 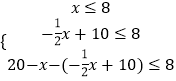 ,
,
解得:4≤x≤8,
∵y是整数,
∴x是偶数,
∴x=4,6,8,共三个值,因而有三种安排方案.
方案一:4车装运A,8车装运B,8车装运C;
方案二:6车装运A,7车装运B,7车装运C;
方案三:8车装运A,6车装运B,6车装运C;
(3)解:设绿化费用为w元,由(1)知
w=20x×40+50(﹣ ![]() x+10)×48+30(20﹣x+
x+10)×48+30(20﹣x+ ![]() x﹣10)×32,
x﹣10)×32,
整理,得w=﹣880x+33600,
∵﹣880<0,
∴w随x的增大而减小,
∴当x=8时,w的值最小,最小值为:﹣880×8+33600=26560元.
故采用(2)中的第三个方案,即8车装运A,6车装运B,6车装运C.
【解析】(1)由“A,B,C三种绿化树共800株”可得40x+48y+32(20﹣x﹣y)=800,变形为y=﹣ ![]() x+10;(2)由“装运每种绿化树的车辆数都不多于8辆”可翻译为不等式组x≤8,y≤8,20xy≤8,y代换为x的代数式,即可求出x的范围,在整数范围内有几个值,就有几种方案;(3)
x+10;(2)由“装运每种绿化树的车辆数都不多于8辆”可翻译为不等式组x≤8,y≤8,20xy≤8,y代换为x的代数式,即可求出x的范围,在整数范围内有几个值,就有几种方案;(3)

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案