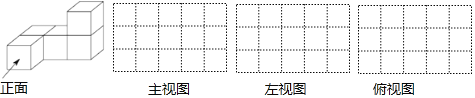
��Ŀ����
����Ŀ����ͼ���������ϵ�ԭ�㿪ʼ���������ƶ�2cm����A�㣬�������ƶ�4cm����B�㣬Ȼ�������ƶ�10cm����C�㣮
![]()
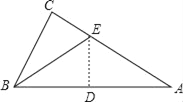
��1����1����λ���ȱ�ʾ1cm�����������������������ϱ�ʾ��A��B��C�����λ�ã�
��2���ѵ�C����A�ľ����ΪCA����CA��______cm��
��3������B��ÿ��3cm���ٶ������ƶ���ͬʱA��C����ÿ��lcm��5cm���ٶ������ƶ������ƶ�ʱ��Ϊt��t��0���룬��̽��CA��AB��ֵ�Ƿ������t�ı仯���ı䣿��˵�����ɣ�
���𰸡���1����ͼ��ʾ������������2��CA��6cm����3��CA��AB��ֵ��������t�ı仯���仯�����ɼ�����.
��������
��1�����������ϵ���ƶ����ɣ��������ϱ�ʾ��A��B��C��λ�ü��ɣ���2�����������������ľ��빫ʽ���CA�ij����ɣ���3�����ƶ�ʱ��Ϊt��ʱ����ʾ��A��B��C��ʾ���������CA-AB��ֵ���������жϣ�
��1����ͼ��ʾ��
![]()
��2��CA��4������2����4+2��6��cm����
�ʴ�Ϊ��6��
��3��CA��AB��ֵ��������t�ı仯���仯���������£�
��������ã�CA����4+5t��������2+t����6+4t��AB������2+t��������6��3t����4+4t��
��CA��AB����6+4t������4+4t����2��
��CA��AB��ֵ��������t�ı仯���仯��

����Ŀ���ڡ����ǡ�ͬ����У�ΪŬ�������н��ɡ������ֳ��С����̻���˾�ƻ�����A��B��C�����̻�����800�꣬��20������һ���˻أ������г����½���·�����̻������ƻ���20��������Ҫװ�ˣ�ÿ������ֻ��װ��ͬһ���̻������ұ���װ���������±��ṩ����Ϣ������������⣺
�� �� �� Ʒ �� | A | B | C |
ÿ���������������꣩ | 40 | 48 | 32 |
ÿ������ļ۸�Ԫ�� | 20 | 50 | 30 |
��1����װ��A���̻����ij�����Ϊx��װ��B���̻����ij�����Ϊy����y��x֮��ĺ�����ϵʽ��
��2�����װ��ÿ���̻����ij�������������8������ô�����İ��ŷ����м��֣���д��ÿ�ְ��ŷ�����
��3�����ڡ����ǡ�ͬ�����Ҫ�����н�Լ����ʵ�£���Ӧ���ã�2���е����ְ��ŷ�����Ϊʲô��