题目内容
【题目】A、B是数轴上两点,点A对应的数是-2,点B对应的数是2. △ABC是等边三角形,D是AB中点. 点M在AC边上,且AM=3CM.
(1)求CD长.
(2)点P是CD上的动点,确定点P使得PM+PA的值最小,并求出PM+PA的最小值.
(3)过点M的直线与数轴交于点Q,且QM![]() .点Q对应的数是t,结合图形直接写出t的取值范围.
.点Q对应的数是t,结合图形直接写出t的取值范围.

【答案】(1)CD=![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据等边三角形的性质及勾股定理进行计算即可;
(2)根据轴对称确定点P,然后取AC的中点为E,连接BE,再利用等边三角形的性质,线段之间的关系及勾股定理进行计算即可;
(3)画出图形,先确定QM=![]() 时,点Q对应的数,最后再根据得到的数写出范围.
时,点Q对应的数,最后再根据得到的数写出范围.
解:(1)∵△ABC是等边三角形,D是AB中点,
∴CD⊥AB,AD=DB,
∵点A、点B对应的数分别是-2和2,
∴AB=4,
∴AC=4,AD=2,
∴在Rt△ACD中,CD=![]() ;
;
(2)连接MB,MB与CD的交点即为所求的P点.
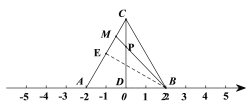
设AC的中点为E,连结BE,
∵△ABC是等边三角形,
∴BE⊥AC,CE=2,
∵AM=3CM,
∴CM=1,AM=3,
∴EM=1,
由三角形面积相等,底相等可得:BE=CD=![]() ,
,
∴在Rt△BEM中,BM=![]() ,
,
即PM+PA的最小值为![]() ;
;
(3)如图,QM=![]() ,过点M作ME⊥AB于点E,
,过点M作ME⊥AB于点E,

∵CD⊥AB,
∴ME∥CD,
∴△AEM∽△ADC,
∴![]() ,
,
又∵AD=2,CD=![]() ,
,
∴AE=![]() ,ME=
,ME=![]() ,
,
∴DE=![]() ,
,
∵点Q对应的数是t,
∴QE=![]() ,
,
∴在Rt△MEQ中,![]() ,
,
解得t=4或-5,
∵QM![]() ,
,
∴![]() 或
或![]() .
.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目