题目内容
【题目】在平面直角坐标系![]() 中,有一抛物线
中,有一抛物线![]() ,与
,与![]() 轴交于点
轴交于点![]() 、点
、点![]() ,现将背面完全相同,正面分别标有数
,现将背面完全相同,正面分别标有数![]() 、
、![]() 、
、![]() 、
、![]() 的
的![]() 张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点
张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点![]() 的横坐标,将该数的平方作为点
的横坐标,将该数的平方作为点![]() 的纵坐标,则点
的纵坐标,则点![]() 落在抛物线与
落在抛物线与![]() 轴围成的区域内(含边界)的概率为________.
轴围成的区域内(含边界)的概率为________.
【答案】![]()
【解析】
首先求出抛物线与坐标轴的交点,进而画出函数图象,再得出P坐标,进而判断P点位置求出概率.
当y=0,则0=-x2+2x+3,
解得:x1=-1,x2=3,
故抛物线与x轴交点为:(-1,0),(3,0),
当x=0,则y=3,则抛物线与y轴交点为:(0,3),
y=-x2+2x+3
=-(x-1)2+4,
故抛物线顶点坐标为:(1,4),
如图所示:
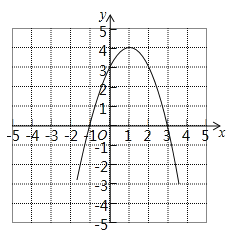
∵现将背面完全相同,正面分别标有数-1、0、1、2的4张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,将该数的平方作为点P的纵坐标,
∴P点坐标为:(-1,1),(0,0),(1,1),(2,4),
如图所示:(-1,1)一定不在抛物线与x轴围成的区域内;
(0,0),(1,1)一定在抛物线与x轴围成的区域内;
当x=2时,y=3,则(2,4)一定不在抛物线与x轴围成的区域内,
故点P落在抛物线与x轴围成的区域内(含边界)的概率为![]() .
.
故答案是:![]() .
.

练习册系列答案
相关题目