题目内容
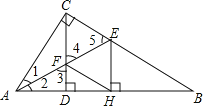
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.
求证:(1)CF=CE
(2)四边形CFHE是平行四边形.
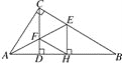
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用垂直的定义结合角平分线的性质以及互余的性质得出∠4=∠5,进而得出答案;
(2)根据题意分别得出CF∥EH,CF=EH,进而得出答案.
证明 (1)如图所示:∵∠ACB=90°,CD⊥AB垂足为D,
∴∠1+∠5=90°,∠2+∠3=90°,
又∵∠AE平分∠CAB,
∴∠1=∠2,
∴∠3=∠5,
∵∠3=∠4,
∴∠4=∠5,
∴CF=CE;
(2)∵AE平分∠CAB,CE⊥AC,EH⊥AB,
∴CE=EB,
由(1)知,CF=CE,
∴CF=EH,
∵CD⊥AB,EH⊥AB,
∴∠CDB=90°,∠EHB=90°,
∴∠CDB=∠EHB,
∴CD∥EH,
即CF∥EH,
∴四边形CFHE是平行四边形.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目