题目内容
【题目】如图,在平面直角坐标系xOy中,直线AP交x轴于点P(p,0),交y轴于点A(0,a),且a、p满足![]() .
.
(1)求直线AP的解析式;
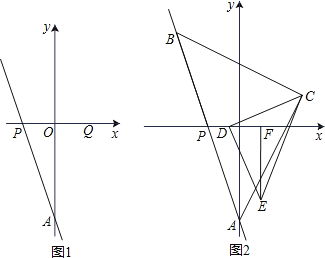
(2)如图1,点P关于y轴的对称点为Q,R(0,2),点S在直线AQ上,且SR=SA,求直线RS的解析式和点S的坐标;
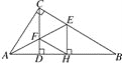
(3)如图2,点B(﹣2,b)为直线AP上一点,以AB为斜边作等腰直角三角形ABC,点C在第一象限,D为线段OP上一动点,连接DC,以DC为直角边,点D为直角顶点作等腰三角形DCE,EF⊥x轴,F为垂足,下列结论:①2DP+EF的值不变;②![]() 的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.
的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.
【答案】(1)y=﹣3x﹣3;(2)S(![]() ,﹣
,﹣![]() ), y=﹣3x+2;(3)②;定值为
), y=﹣3x+2;(3)②;定值为![]() .
.
【解析】
(1)根据非负数的性质列式求出a、p的值,从而得到点A、P的坐标,然后利用待定系数法求直线的解析式;
(2)根据关于y轴的点的对称求出点Q的坐标,再利用待定系数法求出直线AQ的解析式,设出点S的坐标,然后利用两点间的距离公式列式进行计算即可求出点S的坐标,再利用待定系数法求解直线RS的解析式;
(3)根据点B的横坐标为-2,可知点P为AB的中点,然后求出点B得到坐标,连接PC,过点C作CG⊥x轴于点G,利用角角边证明△APO与△PCG全等,根据全等三角形对应边相等可得PG=AO,CG=PO,再根据△DCE是等腰直角三角形,利用角角边证明△CDG与△EDF全等,根据全等三角形对应边相等可得DG=EF,然后用EF表示出DP的长度,然后代入两个结论进行计算即可找出正确的结论并得到定值.
(1)根据题意得,a+3=0,p+1=0,
解得a=﹣3,p=﹣1,
∴点A、P的坐标分别为A(0,﹣3)、P(﹣1,0),
设直线AP的解析式为y=mx+n,
则![]() ,
,
解得![]() ,
,
∴直线AP的解析式为y=﹣3x﹣3;
(2)根据题意,点Q的坐标为(1,0),
设直线AQ的解析式为y=kx+c,
则![]() ,
,
解得![]() ,
,
∴直线AQ的解析式为y=3x﹣3,
设点S的坐标为(x,3x﹣3),
则SR=![]() ,
,
SA=![]() ,
,
∵SR=SA,
∴![]() =
=![]() ,
,
解得x=![]() ,
,
∴3x﹣3=3×![]() ﹣3=﹣
﹣3=﹣![]() ,
,
∴点S的坐标为S(![]() ,﹣
,﹣![]() ),
),
设直线RS的解析式为y=ex+f,
则 ,
,
解得![]() ,
,
∴直线RS的解析式为y=﹣3x+2;
(3)∵点B(﹣2,b),
∴点P为AB的中点,
连接PC,过点C作CG⊥x轴于点G,
∵△ABC是等腰直角三角形,
∴PC=PA=![]() AB,PC⊥AP,
AB,PC⊥AP,
∴∠CPG+∠APO=90°,∠APO+∠PAO=90°,
∴∠CPG=∠PAO,
在△APO与△PCG中,
 ,
,
∴△APO≌△PCG(AAS),
∴PG=AO=3,CG=PO,
∵△DCE是等腰直角三角形,
∴CD=DE,∠CDG+∠EDF=90°,
又∵EF⊥x轴,
∴∠DEF+∠EDF=90°,
∴∠CDG=∠DEF,
在△CDG与△EDF中,
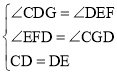 ,
,
∴△CDG≌△EDF(AAS),
∴DG=EF,
∴DP=PG﹣DG=3﹣EF,
①2DP+EF=2(3﹣EF)+EF=6﹣EF,
∴2DP+EF的值随点D的变化而变化,不是定值,
②![]() ,
,
![]() 的值与点D的变化无关,是定值
的值与点D的变化无关,是定值![]() .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案