题目内容
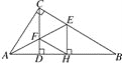
【题目】在矩形ABCD中,AB=3,AD=4,将△ABD沿着BD折叠,使点A与点E重合.
(1)如图,对角线AC、BD相交于点O,连接OE,则线段OE的长= ;
(2)如图,过点E作EF∥CD交线段BD于点F,连接AF,求证:四边形ABEF是菱形;
(3)如图,在(2)条件下,线段AE、BD相交于M,连接CE,求线段CE的长.
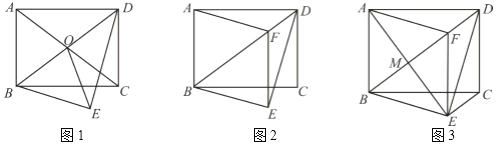
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)根据翻折的特点知OE=OA,由勾股定理求出AC即可求出OA;
(2)先证明四边形ABEF是平行四边形,再由翻折知AB=BE,即可得到四边形ABEF是菱形;
(3)先在(2)的前提下,求出BM的长,从而得到BF的长,然后求出DF,再证明出四边形DFEC是平行四边形即可得到EC=DF=![]() .
.
解:(1) ![]() .
.
由翻折知识知:OE=OA,
∵OA=![]() ,AC=
,AC=![]() , AB=3,AD=4,
, AB=3,AD=4,
∴AC=5,
∴OE= OA=![]() =
=![]() ,
,
故答案为:![]() .
.
(2)证明:
∵ 四边形ABCD是菱形,
∴ AB∥CD,
∵ EF∥CD,
∴ AB∥EF ,
∴ ∠ABF=∠BFE,
由翻折性质可得:
∠ABF=∠EBF,AB=BE ,
∴ ∠BFE=∠EBF,
∴ BE=FE,
∵ AB=BE,
∴ AB=FE,
∵ AB∥EF,
∴ 四边形ABEF是平行四边形,
又∵ BE=FE,
∴ 平行四边形ABEF是菱形;
(3)如图,∵平行四边形ABEF是菱形,
∴ AE⊥BD,BM=FM,
![]() ,
,
∴ ![]() ,
,
∴ AM=![]() ,
,
∴ 根据勾股定理得BM=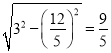 ,
,
∴ BF=2BM=![]() ∴ DF=BD-BF=
∴ DF=BD-BF=![]() ,
,
∵ EH∥CD,EF=CD,
∴ 四边形EFCD是平行四边形,
∴ CE=DF=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目