题目内容
【题目】如图，四边形ABCD是矩形，把矩形沿对角线AC折叠，点B落在点E处，CE与AD相交于点O．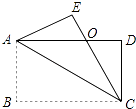 
（1）求证：△AOE≌△COD；
（2）若∠OCD=30°，AB= 
，求△AOC的面积．
【答案】
（1）证明：∵四边形ABCD是矩形，
∴AB=CD，∠B=∠D=90°，
∵矩形ABCD沿对角线AC折叠点B落在点E处，
∴AB=AE，∠B=∠E，
∴AE=CD，∠D=∠E，
在△AOE和△COD中，
，
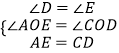∴△AOE≌△COD（AAS）
（2）解：∵△AOE≌△COD，
∴AO=CO，
∵∠OCD=30°，AB= 
，
∴CO=CD÷cos30°= ÷ 
=2，
∴△AOC的面积= 
AOCD= ×2× =
【解析】（1）根据矩形的对边相等可得AB=CD，∠B=∠D=90°，再根据翻折的性质可得AB=AE，∠B=∠E，然后求出AE=CD，∠D=∠E，再利用“角角边”证明即可；（2）根据全等三角形对应边相等可得AO=CO，解直角三角形求出CO，然后利用三角形的面积公式列式计算即可得解．
练习册系列答案
名校课堂系列答案
相关题目
