题目内容
【题目】(1)如图(1)在RtΔABC中,∠ACB=900,∠B=600,在图中作出∠ACB的三等分线CD,CE.(要求:尺规作图,保留痕迹,不定作法)
(2)由(1)知,我们可以用尺规作出直角的三等分线,但是仅仅使用尺规却不能把任意一个角分成三等分,为此,人们发明了许多等分角的机械器具,如图(2)是用三张硬纸片自制的一个最简单的三分角器,与半圆O相接的AB带的长度与半圆的半径相等:BD带的长度任意,它的一边与直线AC形成一个直角,且志半圆相切于点B,假设需要将∠KSM三等分,如图(3),首先将角的顶点S置于BD上,角的一边SK经过点A,另一边SM与半圆相切,连接SO,则SB,SO为∠KSM的三等分线,请你证明。

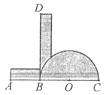

图(1) 图(2) 图(3)
【答案】见解析
【解析】试题分析:(1)如图射线CD、CE为所求是三等分线;
(2)如图,设SM与半圆O相切于点N,连接ON.则∠ONS=90°,只要证明△SBA≌△SBO,△SOB≌△SON,即可解决问题;
试题解析:
(1)如图射线CD、CE为所求是三等分线.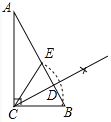
(2)如图,设SM与半圆O相切于点N,连接ON.则∠ONS=90°,
∵DB⊥AC,DB与半圆相切于点BM,
∴∠ABS=∠OBS=90°,
∵BA=BO.SB=SB,
∴△SBA≌△SBO,
∴∠ASB=∠BSO,
∵SO=SO.OB=ON,∠SBO=∠SNO,
∴△SBO≌△SNO,
∴∠BSO=∠OSN,
∴∠ASB=∠BSO=∠OSC,
∴SB,SO为∠KSM的三等分线.

练习册系列答案
相关题目