题目内容
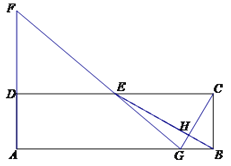
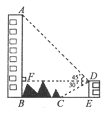
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为300,测得大楼顶端 A的仰角为450(点B,C,E在同一水平直线上)。已知AB=50m,DE=10m,求障碍物B,C两点间的距离。(结果精确到1m,参考数据: ![]() )
)

【答案】障碍物B,C两点间的距离约为23 m
【解析】试题分析:过点D作DF⊥AB于点F,过点C作CH⊥DF于点H,则DE=BF=CH=20m,根据直角三角形的性质得出DF的长,在Rt△CDE中,利用锐角三角函数的定义得出CE的长,根据BC=BE-CE即可得出结论.
试题解析:
过点D作DF⊥AB交于AB于点F,则∠DFA=900,∠ADA=450,∠FDC=300,
∵AB⊥BE于点B,DE⊥BE于点E,
∴∠BFD=∠FBE=∠BED=900.
∴四边形BEDF是矩形
∴BF=DE,FD=BE,FD∥BE.
∵AB=50,DE=10,
∴AF=AB-BF=40
在RtΔAFD中, ![]() ,
,
∴DF=AF=40
∵FD∥BE,∴∠DCE=∠FDC=300.
在RtΔCDE中![]() ,
,
∴![]()
∴![]()
答:障碍物B,C两点间的距离约为23m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】根据下表,回答问题:
x | … | -2 | -1 | 0 | 1 | 2 | … |
-2x+5 | … | 9 | 7 | 5 | 3 | a | … |
2x+8 | … | 4 | 6 | 8 | 10 | b | … |
(初步感知)
(1)a= ;b= ;
(归纳规律)
(2)随着x值的变化,两个代数式的值变化规律是什么?
(问题解决)
(3)比较-2x+5与2x+8的大小;
(4)请写出一个含x的代数式,要求x的值每增加1,代数式的值减小5,当x=0时,
代数式的值为-7.