Question

如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE． (1)求证：CE＝CF． (2)若点G在AD上，且∠GCE＝45°，则GE＝BE＋GD成立吗？为什么？

Answer 1

答案：
解析：

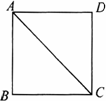
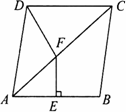
(1)证明：在正方形ABCD中， 　　BC＝DC，∠B＝∠CDF， 　　又∵BE＝DF， 　　∴△CBE≌△CDF． 　　∴CE＝CF． 　　(2)解：GE＝BE＋GD成立． 　　理由如下：由(1)得：△CBE≌△CDF， 　　∴∠BCE＝∠DCF，BE＝DF． 　　∴∠BCE＋∠ECD＝∠DCF＋∠ECD，即∠ECF＝∠BCD＝90°， 　　又∠GCE＝45°，∴∠GCF＝∠GCE＝45°． 　　∵CE＝CF，∠GCE＝∠GCF，GC＝GC， 　　∴△ECG≌△FCG．∴GE＝GF． 　　∴GE＝DF＋GD＝BE＋GD．