题目内容
如图,直线 与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .
与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .

 与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .
与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .
(7,3).
试题分析:旋转不改变图形的大小和性质,所得图形与原图形全等,根据全等三角形的性质,即可得到相应线段的长.
试题解析:直线y=-
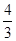 x+4与x轴,y轴分别交于A(3,0),B(0,4)两点.
x+4与x轴,y轴分别交于A(3,0),B(0,4)两点.旋转前后三角形全等.
由图易知点B′的纵坐标为OA长,即为3,
∴横坐标为OA+OB=OA+O′B′=3+4=7.
∴点B′的坐标为(7,3).
考点: 1.坐标与图形变化-旋转;2.一次函数的性质.

练习册系列答案
相关题目


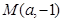 和
和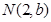 不重合.
不重合.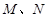 关于_______对称时,
关于_______对称时,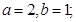
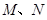 关于原点对称时,
关于原点对称时,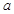 =__________,
=__________,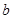 =_________.
=_________. ,
, ,∠
,∠ ,∠
,∠ ,求
,求 、
、 两点的坐标.
两点的坐标.