��Ŀ����
����Ŀ����֪���κ���y=ax2��ͼ���㣨2��1����
��1������κ���y=ax2�Ľ���ʽ��
��2��һ�κ���y=mx+4��ͼ������κ���y=ax2��ͼ���ڵ�A��x1��y1����B��x2��y2�����㣮
�ٵ�m=![]() ʱ��ͼ�٣�����֤����AOBΪֱ�������Σ�
ʱ��ͼ�٣�����֤����AOBΪֱ�������Σ�
�����жϵ�m��![]() ʱ��ͼ�ڣ�����AOB����״����֤���� n>S����DOE��ü��ɣ�
ʱ��ͼ�ڣ�����AOB����״����֤���� n>S����DOE��ü��ɣ�
��3�����ݵ�2�ʣ�˵��һ�����ܵõ��Ľ��ۣ�����Ҫ��֤����
���𰸡�
��1��
����𡿣�1���⣺��y=ax2���㣨2��1����
��1=4a�����a=![]() ��
��
�������߽���ʽΪy=![]() x2��
x2��
��2��
��֤����
��m=![]() ʱ������ֱ�ߺ������߽���ʽ�ɵ�
ʱ������ֱ�ߺ������߽���ʽ�ɵ� �����
�����![]() ��
��![]() ��
��
��A����2��1����B��8��16����
�ֱ��A��B��AC��x�ᣬBD��x�ᣬ����ֱ�ΪC��D����ͼ1��

��AC=1��OC=2��OD=8��BD=16��
��![]() ���ҡ�ACO=��ODB��
���ҡ�ACO=��ODB��
���ACO�ס�ODB��
���AOC=��OBD��
�֡ߡ�OBD+��BOD=90�㣬
���AOC+��BOD=90�㣬����AOB=90�㣬
���AOBΪֱ�������Σ�
�ڽ⣺��AOBΪֱ�������Σ�
֤�����£�
��m��![]() ʱ������ֱ�ߺ������߽���ʽ�ɵ�
ʱ������ֱ�ߺ������߽���ʽ�ɵ� �����
����� ��
��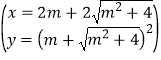 ��
��
��A��2m��2![]() ����m��
����m��![]() ��2����B��2m+2
��2����B��2m+2![]() ����m+
����m+![]() ��2����
��2����
�ֱ��A��B��AC��x�ᣬBD��x�ᣬ��ͼ2��

��AC=��m��![]() ��2��OC=����2m��2
��2��OC=����2m��2![]() ����BD=��m+
����BD=��m+![]() ��2��OD=2m+2
��2��OD=2m+2![]() ��
��
��![]() ���ҡ�ACO=��ODB��
���ҡ�ACO=��ODB��
���ACO�ס�OBD��
���AOC=��OBD��
�֡ߡ�OBD+��BOD=90�㣬
���AOC+��BOD=90�㣬����AOB=90�㣬
���AOBΪֱ�������Σ�
��3��
�⣺��2��֪��һ�κ���y=mx+4��ͼ������κ���y=ax2�Ľ���ΪA��B�����AOB��Ϊֱ�������Σ����𰸲�Ψһ����
����������1���ѵ㣨2��1����������a��ֵ������������ߵĽ���ʽ��
��2���ٿ������A��B��������꣬��A��B������x��Ĵ��ߣ����������֤����ACO�ס�ODB����֤����AOB=90�㣬���ж���AOBΪֱ�������Σ��ڿ���m�ֱ��ʾ��A��B��������꣬��A��B������x��Ĵ��ߣ���ʾ��AC��BD�ij�����֤����ACO�ס�ODB����������ɵõ���AOB=90�㣬���ж���AOBΪֱ�������Σ�
��3����ϣ�2���Ĺ��̿ɵõ���AOB��Ϊֱ�������εȽ��ۣ�







