题目内容
【题目】
(1)(1)如图1是某个多面体的表面展开图.
①请你写出这个多面体的名称,并指出图中哪三个字母表示多面体的同一点;
②如果沿BC、GH将展开图剪成三块,恰好拼成一个矩形,那么△BMC应满足什么条件?(不必说理)
(2)如果将一个三棱柱的表面展开图剪成四块,恰好拼成一个三角形,如图2,那么该三棱柱的侧面积与表面积的比值是多少?为什么?(注:以上剪拼中所有接缝均忽略不计)
【答案】
(1)
解:①根据这个多面体的表面展开图,可得
这个多面体是直三棱柱,
点A、M、D三个字母表示多面体的同一点.
②△BMC应满足的条件是:
a、∠BMC=90°,且BM=DH,或CM=DH;
b、∠MBC=90°,且BM=DH,或BC=DH;
c、∠BCM=90°,且BC=DH,或CM=DH;
(2)
解:如图2,连接AB、BC、CA
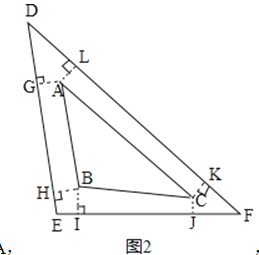
∵△DEF是由一个三棱柱表面展开图剪拼而成,
∴矩形ACKL、BIJC、AGHB为棱柱的三个侧面,
且四边形DGAL、EIBH、FKCJ须拼成与底面△ABC全等的另一个底面的三角形,
∴AC=LK,且AC=DL+FK,
∴![]() ,
,
同理,可得
![]() ,
,
∴△ABC∽△DEF,
∴![]() ,
,
即S△DEF=4S△ABC,
∴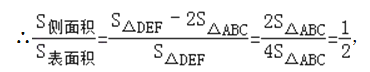 ,
,
即该三棱柱的侧面积与表面积的比值是![]() .
.
【解析】(1)①根据这个多面体的表面展开图,可得这个多面体是直三棱柱,点A、M、D三个字母表示多面体的同一点,据此解答即可.
②根据图示,要使沿BC、GH将展开图剪成三块,恰好拼成一个矩形,则△BMC应满足两个条件:△BMC中的三个内角有一个是直角;△BMC中的一条直角边和DH的长度相等,据此解答即可.
(2)首先判断出矩形ACKL、BIJC、AGHB为棱柱的三个侧面,且四边形DGAL、EIBH、FKCJ须拼成与底面△ABC全等的另一个底面的三角形,AC=LK,且AC=DL+FK,![]() ,同理,可得
,同理,可得![]() ,据此判断出△ABC∽△DEF,即可判断出S△DEF=4S△ABC;然后求出该三棱柱的侧面积与表面积的比值是多少即可.
,据此判断出△ABC∽△DEF,即可判断出S△DEF=4S△ABC;然后求出该三棱柱的侧面积与表面积的比值是多少即可.
【考点精析】利用二次函数图象的平移对题目进行判断即可得到答案,需要熟知平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案