题目内容
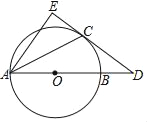
【题目】如图,![]() 是⊙
是⊙![]() 的弦,
的弦,![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() 是⊙
是⊙![]() 的切线.
的切线.
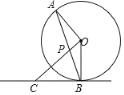
(1)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)若![]() ,求
,求![]() 的长;
的长;
(3)设![]() 的面积是
的面积是![]() 的面积是
的面积是![]() ,且
,且![]() .若⊙
.若⊙![]() 的半径为
的半径为![]() ,求
,求![]() .
.
【答案】(1)![]() 是等腰三角形,理由见解析;(2)
是等腰三角形,理由见解析;(2)![]() 的长为
的长为![]() ;(3)
;(3)![]() .
.
【解析】
(1)首先连接OB,根据等腰三角形的性质由OA=OB得![]() ,由点C在过点B的切线上,且
,由点C在过点B的切线上,且![]() ,根据等角的余角相等,易证得∠PBC=∠CPB,即可证得△CBP是等腰三角形;
,根据等角的余角相等,易证得∠PBC=∠CPB,即可证得△CBP是等腰三角形;
(2)设BC=x,则PC=x,在Rt△OBC中,根据勾股定理得到![]() ,然后解方程即可;
,然后解方程即可;
(3)作CD⊥BP于D,由等腰三角形三线合一的性质得![]() ,由
,由![]() ,通过证得
,通过证得![]() ,得出
,得出![]() 即可求得CD,然后解直角三角形即可求得.
即可求得CD,然后解直角三角形即可求得.
(1)![]() 是等腰三角形,理由:
是等腰三角形,理由:
连接![]() ,
,
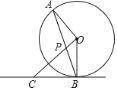
![]()
![]()
![]() ⊙
⊙![]() 与
与![]() 相切与点
相切与点![]() ,
,
![]() ,即
,即![]() ,
,![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]() 是等腰三角形
是等腰三角形
(2)设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,
,
即![]() 的长为
的长为![]() ;
;
(3)解:作![]() 于
于![]() ,
,
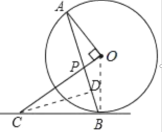
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目