题目内容
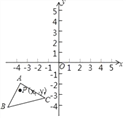
【题目】如图，已知抛物线与x轴交于A（﹣1，0）、B（4，0）两点，与y轴交于点C（0，3）．
（1）求抛物线的解析式；
（2）在x轴下方的抛物线上是否存在一点P，使△PAB的面积等于△ABC的面积？若存在，求出点P的坐标；若不存在，请说明理由．
【答案】（1）y=
（2）存在一点P，使△PAB的面积等于△ABC的面积
【解析】试题分析：（1）设抛物线的解析式为y=ax2+bx+c，代入三点即求得方程式；
（2）由△ABC的底边AB上的高为3，设△PAB的高为h，则|h|=3，则点P的纵坐标为3或-3，然后根据点P在x轴的下方，可知纵坐标只能为-3，然后代入求解一元二次方程即可．
试题解析：（1）设抛物线的解析式为y=ax2+bx+c，
∵抛物线与y轴交于点C的坐标（0，3），
∴y=ax2+bx+3，
又∵抛物线与x轴交于点A（﹣1，0）、B（4，0），
∴
，
∴抛物线的解析式为
；
（2）存在一点P，使△PAB的面积等于△ABC的面积，
∵△ABC的底边AB上的高为3，
设△PAB的高为h，则|h|=3，又点P在x轴下方，∴点P的纵坐标为﹣3，
，
∴点P的坐标为
，
，
练习册系列答案
黄冈小状元同步计算天天练系列答案
相关题目
【题目】在体育课上，对七年级男生进行引体向上测试.以做4个为标准，超过的个数记作正数，不足的个数记作负数其中8名男生做引体向上的个数记录如下：
+3 | －1 | 1 | +3 | 1 | 0 | +2 | －1 |
这8名男生平均每人做了多少个引体向上？
