��Ŀ����
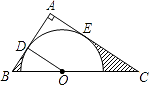
����Ŀ���ı���ABCD�������Σ��Խ���AC��BD�ཻ�ڵ�O��
��1����ͼ1����P��������ABCD��һ�㣬����OP����OPΪһ�ߣ���������OPMN���ұ�ON���BC�ཻ������AP��BN��
�������ⲹȫͼ1��
���ж�AP��BN��������ϵ��λ�ù�ϵ��д�����۲�����֤����
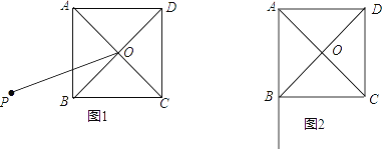
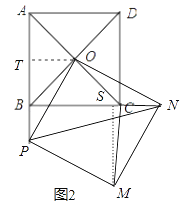
��2����P��AB�ӳ����ϣ�����APO=30��������OP����OPΪһ�ߣ���������OPMN���ұ�ON��BC���ӳ���ǡ���ڵ�N������CM����AB=2����CM�ij�������д����������������CM���Ĺ��̣�
���𰸡���1����ͼ�μ�������AP=BN��AP��BN��2��������
��������������(1)���ٸ�����������ͼ�μ��ɣ��ڽ��ۣ�AP=BN��AP��BN��ֻҪ֤����APO�ա�BNO���ɣ�(2)����RT��CMS�У����SM��SC���ɽ�����⣮
��⣺(1)���⣺�ٲ�ȫͼ����ͼ1��ʾ��
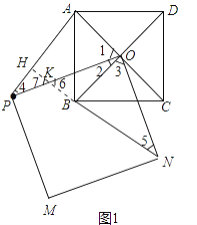
�ڽ��ۣ�AP=BN��AP��BN��
���ɣ��ӳ�NB��AP��H����OP��K�� ���ı���ABCD�������Σ� ��OA=OB��AO��BO��
���1+��2=90�㣬 ���ı���OPMN�������Σ� ��OP=ON����PON=90�㣬 ���2+��3=90�㣬
���1=��3�� �ڡ�APO�͡�BNO���� �� ���APO�ա�BNO�� ��AP=BN�����4=��5��
�� ���APO�ա�BNO�� ��AP=BN�����4=��5��
�ڡ�OKN������5+��6=90�㣬 �ߡ�7=��6�� ���4+��7=90�㣬 ���PHK=90�㣬 ��AP��BN��
(2)���⣺����˼·���£�
a������֤����APO�ա�BNO��AP=BN����OPA=ONB��
b����OT��AB��T��MS��BC��S���������֪AT=TB=1��
c���ɡ�APO=30�㣬�ɵ�PT= ![]() ��BN=AP=
��BN=AP= ![]() +1���ɵá�POT=��MNS=60�㣮
+1���ɵá�POT=��MNS=60�㣮
d���ɡ�POT=��MNS=60�㣬OP=MN��
��֤����OTP�ա�NSM�� ��PT=MS= ![]() �� ��CN=BN��BC=
�� ��CN=BN��BC= ![]() ��1��
��1��
��SC=SN��CN=2�� ![]() �� ��RT��MSC��CM2=MS2+SC2 �� ��MC�ij�������
�� ��RT��MSC��CM2=MS2+SC2 �� ��MC�ij�������