题目内容
【题目】等边![]() 的边长为3,在边
的边长为3,在边![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,以
,以![]() 为一边作等边
为一边作等边![]() ,连接
,连接![]() ,则线段
,则线段![]() 的长为__________.
的长为__________.
【答案】2或![]()
【解析】
分两种情况:①当C1在A1B的上方时,证明△A1BC≌△ABC1,则A1C=AC1=2;②当C1在A1B的下方时,作辅助线,构建全等三角形和直角三角形,同理得:△ABA1≌△CBC1,则C1C=A1A=1,∠C1CB=∠BAC=60°,得到30°的Rt△C1CD,根据性质求得CD=![]() ,C1D=
,C1D=![]() ,最后利用勾股定理可得结论.
,最后利用勾股定理可得结论.
分两种情况:
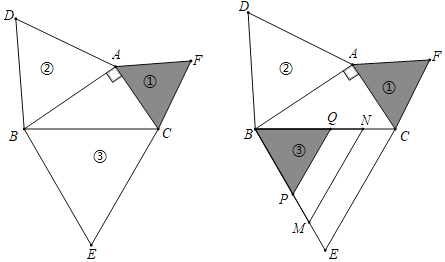
① 当C1在A1B的上方时,如图1,
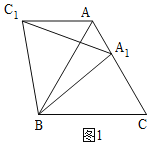
∵AB=3,AA1=2,
∴A1C=3-1=2,
∵△ABC和△A1BC1是等边三角形,
∴AB=BC,A1B=BC1,∠ABC=∠A1BC1=60°,
∴∠A1BC=∠ABC1,
在△A1BC和△ABC1中,
∵BC=AB,∠A1BC=∠C1BA,A1B=C1B,
∴△A1BC≌△ABC1(SAS),
∴A1C=AC1=2;
② 当C1在A1B的下方时,如图2,连接C1C,过C1作C1D⊥AC于D,
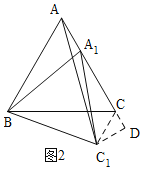
同理得:△ABA1≌△CBC1,
∴C1C=A1A=1,∠C1CB=∠BAC=60°,
∵∠ACB=60°,
∴∠C1CD=60°,
Rt△C1CD中,∠CC1D=30°,
∴CD=![]() C1C=
C1C=![]() ,C1D=
,C1D=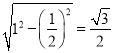 ,
,
Rt△AC1D中,AD=3+![]() =
=![]() ,
,
由勾股定理得:AC1=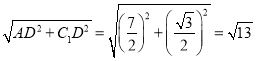 ,
,
综上所述,则线段A1C的长为2或![]() .
.
故答案为:2或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目