题目内容
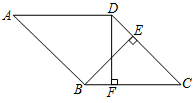
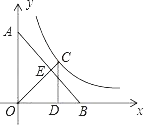
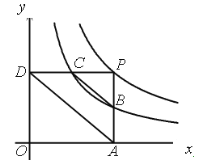
【题目】如图,已知在平面直角坐标系xOy中,O为坐标原点,点P是反比例函数![]()
![]() x
x![]() 的图象上任意一点,PA
的图象上任意一点,PA![]() x轴于点A,PD
x轴于点A,PD![]() y轴于点D,分别交反比例函数
y轴于点D,分别交反比例函数![]()
![]() x
x![]() ,
,![]() k
k![]() 的图象于点B,C
的图象于点B,C![]() 下列结论:①当k
下列结论:①当k![]() 时,BC是
时,BC是![]() PAD的中位线;②不论k为何值,都有
PAD的中位线;②不论k为何值,都有![]() PDA∽
PDA∽![]() PCB;③当四边形ABCD的面积等于2时,k
PCB;③当四边形ABCD的面积等于2时,k![]() ④若点P
④若点P![]() ,将
,将![]() PCB沿CB对折,使得P点恰好落在OA上时,则
PCB沿CB对折,使得P点恰好落在OA上时,则![]() ;其中正确的个数有( )
;其中正确的个数有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①根据反比例函数k的几何意义,可得![]() ,
,![]() ,两直角三角形同底,则面积之比等于高之比,所以PA=2AB,同理可得C是PD的中点,所以BC是
,两直角三角形同底,则面积之比等于高之比,所以PA=2AB,同理可得C是PD的中点,所以BC是![]() 的中位线;
的中位线;![]() 根据题意由三角形的面积可得PA:
根据题意由三角形的面积可得PA:![]() :
:![]() :k,再加上有一个公共角,则两个三角形相似;
:k,再加上有一个公共角,则两个三角形相似;![]() 先求得△PDA的面积,然后再求得△PCB的面积,根据相似三角形的面积等于相似比的平方,求得△PDA与△PCB的相似比,从而可求得k值;
先求得△PDA的面积,然后再求得△PCB的面积,根据相似三角形的面积等于相似比的平方,求得△PDA与△PCB的相似比,从而可求得k值;![]() 首先证明
首先证明![]() ∽
∽![]() ,求出AQ的长,再在直角三角形ABQ中,通过勾股定理求出k的值.
,求出AQ的长,再在直角三角形ABQ中,通过勾股定理求出k的值.
![]() 连接PO、BO,根据题意可知:
连接PO、BO,根据题意可知:![]() ,
,![]() ,
,
![]() ,即B是PA中点,同理可得C是PD的中点,
,即B是PA中点,同理可得C是PD的中点,
![]() 是
是![]() 的中位线.故
的中位线.故![]() 成立.
成立.
![]() 根据题意由三角形的面积可得PA:
根据题意由三角形的面积可得PA:![]() :
:![]() :k,
:k,
![]() :
:![]() :PC,
:PC,![]() ,
,![]() ∽
∽![]() .故
.故![]() 成立.
成立.
![]() 根据题意可知,
根据题意可知,![]() ,
,![]() ,
,![]() ,
,
又由![]() 可知
可知![]() ∽
∽![]() ,
,![]() :
:![]() :
:![]() ,
,![]() :
:![]() :
:![]() ,
,
![]() :
:![]() :6,
:6,![]() ,故
,故![]() 成立.
成立.
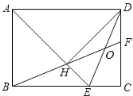
![]() 如下图,
如下图,![]() 沿CB对折到
沿CB对折到![]() ,根据题意可得
,根据题意可得![]() ,
,

![]() 根据
根据![]() 可知
可知![]() ,
,![]() ,
,![]() 可证明
可证明![]() ∽
∽![]() ,
,
![]() :
:![]() :PA,
:PA,![]() ,
,![]() ,
,![]() ,在直角
,在直角![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理列出关于k的方程可解得![]() ,故
,故![]() 不成立.故选C.
不成立.故选C.

练习册系列答案
相关题目