题目内容
【题目】教材的![]() 课题学习
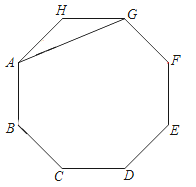
课题学习![]() 要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
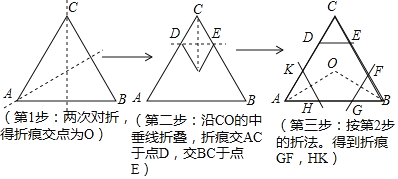
请你根据小明同学的折叠方法,回答以下问题: ![]() 如果设正三角形ABC的边长为a,那么
如果设正三角形ABC的边长为a,那么![]() ______
______ ![]() 用含a的式子表示
用含a的式子表示![]() ;
;
![]() 根据折叠性质可以知道
根据折叠性质可以知道![]() 的形状为______ 三角形;
的形状为______ 三角形;
![]() 请同学们利用
请同学们利用![]() 、
、![]() 的结论,证明六边形KHGFED是一个六边形.
的结论,证明六边形KHGFED是一个六边形.
【答案】 ![]() 等边
等边
【解析】试题分析:(1)根据折叠的性质即可得到结论;
(2)根据折叠的性质即可得到结论;
(3)由(2)知△CDE为等边三角形,根据等边三角形的性质得到CD=CE=DE=![]() CO÷cos30°=
CO÷cos30°=![]() a,求得∠ADE=∠BED=120°,同理可得,AH=AK=KH=
a,求得∠ADE=∠BED=120°,同理可得,AH=AK=KH=![]() a,BG=BF=GF=
a,BG=BF=GF=![]() a,∠CKH=∠BHK=120°,由于AB=BC=AC=a,于是得到结论.
a,∠CKH=∠BHK=120°,由于AB=BC=AC=a,于是得到结论.
试题解析:(1)∵正三角形ABC的边长为a,
由折叠的性质可知,点O是三角形的重心,
∴CO=![]() a;
a;
故答案为: ![]() a;
a;
(2)△CDE为等边三角形;
故答案为:等边;
(3)由(2)知△CDE为等边三角形,
∴CD=CE=DE=![]() CO÷cos30°=
CO÷cos30°=![]() a,
a,
∠ADE=∠BED=120°,
同理可得,AH=AK=KH=![]() a,BG=BF=GF=
a,BG=BF=GF=![]() a,∠CKH=∠BHK=120°,
a,∠CKH=∠BHK=120°,
∵AB=BC=AC=a,
∴DE=DK=KH=HG=GF=FE=![]() a,∠ADE=∠BED=∠CKH=∠BHK=∠CFG=∠AGF=120°,
a,∠ADE=∠BED=∠CKH=∠BHK=∠CFG=∠AGF=120°,
∴六边形KHGFED是一个正六边形.

【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元