题目内容
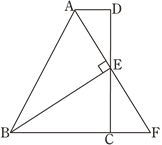
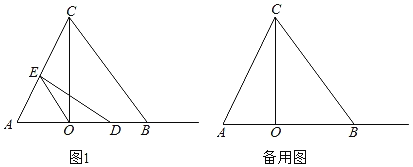
【题目】如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.

(1)求证:△BCF≌△DCE;
(2)若BC=5,CF=3,∠BFC=90°,求DG︰GC的值.
【答案】(1)证明见解析(2)4:3
【解析】
(1)∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°………………………………………………1分
∵△ECF是等腰直角三角形,CE=CF
∴∠FCE=90°
∴∠BCF+∠FCD=∠ECD+∠FCD=90°
∴∠BCF=∠ECD…………………………………………………………3分
∴△BCF≌△DCE;……………………………………………………4分
(2)在Rt△BCF中,∠BFC=90°
∴BF=![]() ……………………………………………5分
……………………………………………5分
∵△BCF≌△DCE
∴DE=BC=4,∠CED=90°
∵△ECF是等腰直角三角形,CE=CF
∴∠CFE=∠CEF=∠DEF=45°………………………………………6分
∵∠CGF=∠DGE
∴△CGF∽△DGE………………………………………………………7分
∴![]() ……………………………………………………8分
……………………………………………………8分
(1)根据四边形ABCD是正方形,可得∠BCF+∠FCD=90°,BC=CD.根据△ECF是等腰直角三角形,CF=CE,可知∠ECD+∠FCD=90度.所以∠BCF=∠ECD.所以△BCF≌△DCE.
(2)在Rt△BFC中,BF=![]() ,所以可知DE=BF=4,∠BFC=∠DEC=∠FCE=90度.得到DE∥FC.可证明△DGE∽△CGF.所以DG:GC=DE:CF=4:3.
,所以可知DE=BF=4,∠BFC=∠DEC=∠FCE=90度.得到DE∥FC.可证明△DGE∽△CGF.所以DG:GC=DE:CF=4:3.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目