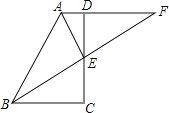
题目内容
【题目】如图,△ABC中,BA=BC,CO⊥AB于点O,AO=4,BO=6.
(1)求BC,AC的长;
(2)若点D是射线OB上的一个动点,作DE⊥AC于点E,连结OE.
①当点D在线段OB上时,若△AOE是以AO为腰的等腰三角形,请求出所有符合条件的OD的长.
②设DE交直线BC于点F,连结OF,CD,若S△OBF:S△OCF=1:4,则CD的长为 (直接写出结果).
【答案】(1)4![]() ;(2)
;(2)![]() 或8
或8![]() .
.
【解析】
根据BA=BC,分别用勾股定理求出CO和AC的长.
①分情况AO=OE和AO=AE,画出图形,根据三角形中位线定理和证明三角形全等解决问题.
②分情况
i)当D在线段OB上时,如图3,过B作BG⊥EF于G,根据同高三角形面积比等于底边之比,得到![]() ,再根据平行线性质∠BDG=∠BFG,得到BD=BF=
,再根据平行线性质∠BDG=∠BFG,得到BD=BF=![]() ,最后使用勾股定理求出结论
,最后使用勾股定理求出结论
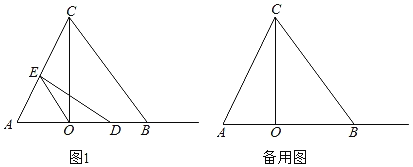
ii)当D在线段OB的延长线上时,如图4,过B作BG⊥DE于G,同理计算可得结论.
解:(1)∵AO=4,BO=6,
∴AB=10,
∵BA=BC,
∴BC=10,
∵CO⊥AB,
∴∠AOC=∠BOC=90°,
由勾股定理得:CO=![]() =
=![]() =8,
=8,
AC=![]() =
=![]() =4
=4![]() ;
;
(2)①分两种情况:
i)如图1,当AO=OE=4时,过O作ON⊥AC于N,
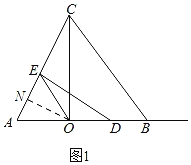
∴AN=EN,
∵DE⊥AC,
∴ON∥DE,
∴AO=OD=4;
ii)当AO=AE=4时,如图2,
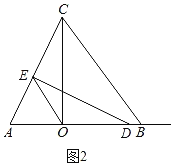
在△CAO和△DAE中,
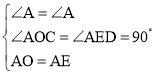 ,
,
∴△CAO≌△DAE(AAS),
∴AD=AC=4![]() ,
,
∴OD=4![]() ﹣4;
﹣4;
②分两种情况:
i)当D在线段OB上时,如图3,过B作BG⊥EF于G,
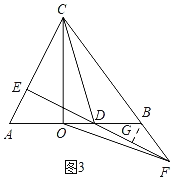
∵S△OBF:S△OCF=1:4,
∴![]()
∴![]()
∵CB=10
∴BF=![]()
∵EF⊥AC,
∴BG∥AC,
∴∠GBF=∠ACB,
∵AE∥BG,
∴∠A=∠DBG,
∵AB=BC,
∴∠A=∠ACB,
∴∠DBG=∠GBF,
∵∠DGB=∠FGB,
∴∠BDG=∠BFG,
∴BD=BF=![]() ,
,
∴OD=OB﹣BD=6﹣![]() =
=![]() ,
,
∴CD=![]() =
=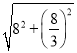 =
=![]() ;
;
ii)当D在线段OB的延长线上时,如图4,过B作BG⊥DE于G,
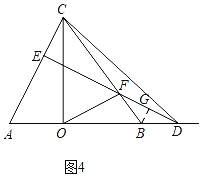
同理得![]() ,
,
∵BC=10,
∴BF=2,
同理得:∠BFG=∠BDF,
∴BD=BF=2,
Rt△COD中,CD=![]() =
=![]() =8
=8![]() ,
,
综上,CD的长为![]() 或8
或8![]() .
.
故答案为:![]() 或8
或8![]() .
.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案