题目内容
【题目】已知等腰△ABC中,AB=AC,∠ABC的平分线交AC于D,过点A作AE // BC交BD的延长线于点E,∠CAE的平分线交BE于点F.
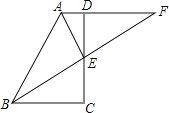
(1)①如图,若∠BAC=36o,求证:BD=EF;
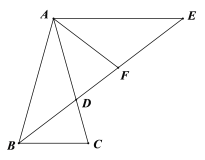
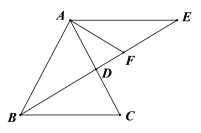
②如图,若∠BAC=60o,求![]() 的值;
的值;
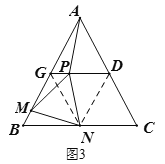
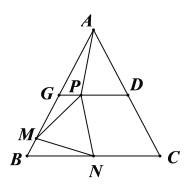
(2)如图,若∠BAC=60o,过点D作DG// BC,交AB于点G,点N为BC中点,点P, M分别是GD, BG上的动点,且∠PNM=60°. 求证:AP=PN=MN.
【答案】(1)①见解析;②![]() ;(2)见解析.
;(2)见解析.
【解析】
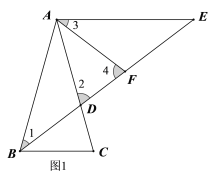
(1)①如图1,根据题意可依次求得∠1=∠E=∠3=36°,∠2=∠4=72°,再根据等腰三角形的判定和等量代换即得结论;
②如图2,根据AB=AC,∠BAC=60°可得△ABC是等边三角形,根据AE // BC和BD是∠ABC的平分线,可得AB=AE,进一步即可求得∠1=∠3=∠E=30°,然后利用30°角的直角三角形的性质可得BD与AB、EF与AE的关系,问题即得解决.
(2)如图3,连接DN、GN,根据题意易得△ADG、△BNG、△GDN为全等的等边三角形,然后利用SAS可证△AGP≌△NGP,从而可得AP=NP,再根据ASA可证△GMN≌△DPN,从而可得MN=PN,问题即得解决.
解:(1)①证明:如图1,∵AB=AC,∠BAC=36°,∴∠ABC=∠ACB=![]() =72°,
=72°,
∵BD是∠ABC的平分线,∴![]() ,
,
∴![]() ,∴BD=AD,
,∴BD=AD,![]() ,
,
∵AE // BC,∴![]() ,
,
∴![]() ,
,
∵AF平分∠DAE,∴![]() ,
,
∴∠3=∠E,
∴AF=EF,![]() ,
,
∴![]() ,∴AD=AF,
,∴AD=AF,
∴BD=EF;
②如图2,∵AB=AC,∠BAC=60°,∴△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD是∠ABC的平分线,∴![]() ,BD⊥AC,
,BD⊥AC,
∴![]() ,∴
,∴![]() ,
,
∵AE // BC,∴![]() ,
,![]() ,
,
∴![]() ,∴AB=AE,
,∴AB=AE,
∵AF平分∠CAE,∴![]() ,
,
∴![]() ,∴FA=FE,
,∴FA=FE,
过点F作FG⊥AE于G,则![]() ,
,
在直角△EFG中,∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]()
∴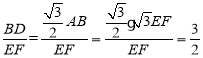 ;
;
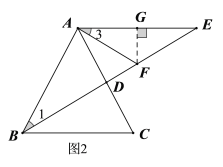
(2)连接DN、GN,如图3,∵AB=AC,∠BAC=60°,∴△ABC是等边三角形,
由上一小题知:D为AC中点,∵DG// BC,∴G为AB中点,
又因为点N为BC中点,则△ADG、△BNG、△GDN为全等的等边三角形,
∴AG=GN,∠AGP=∠NGP=60°,
又∵GP=GP,
∴△AGP≌△NGP(SAS),
∴AP=NP,
∵∠MNP=∠GND=60°,∴∠MNG=∠PND,
又∵GN=DN,∠MGN=∠PDN=60°,
∴△GMN≌△DPN(ASA),
∴MN=PN,
∴AP=PN=MN.