题目内容
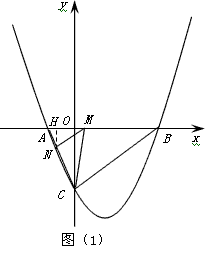
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根。
(1)求抛物线的解析式;
(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连接CM,当△CMN的面积最大时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点F的坐标,若不存在,请说明理由
(1)求抛物线的解析式;
(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连接CM,当△CMN的面积最大时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点F的坐标,若不存在,请说明理由
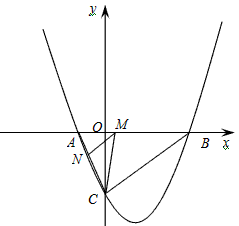
| 解:(1)∵x2-4x-12=0, ∴x1=-2,x2=6, ∴A(-2,0),B(6,0), 又∵抛物线过点A、B、C, 故设抛物线的解析式为y=a(x+2)(x-6),将点C的坐标代入,求得  , ,∴抛物线的解析式为 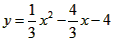 ; ; |
|
| (2)设点M的坐标为(,0),过点N作作NH⊥x轴于点H(如图(1)), ∵点A的坐标为(-2,0),点B的坐标为(6,0), ∴AB=8,AM=m+2, ∵MN∥BC, ∴△MNA∽△ABC, ∴ 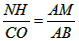 ∴ 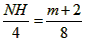 ∴  ∴ 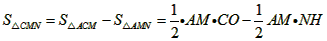 = 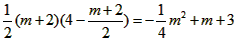 = 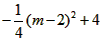 ∴当m=2时,S△CMN有最大值4, 此时,点M的坐标为(2,0); |
 |
(3)∵点D(4,k)在抛物线 上, 上,∴当x=4时,k=-4, ∴点D的坐标是(4,-4), ①如图(2),当AF为平行四边形的边时,AF 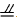 DE, DE,∵D(4,-4), ∴DE=4 ∴F1(-6,0),F2(2,0), ②如图(3),当AF为平行四边形的对角线时,设F(n,0), 则平行四边形的对称中心为( 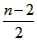 ,0), ,0),∴E'的坐标为(n-6,4), 把E'(n-6,4)代入  ,得n2-16n+36=0, ,得n2-16n+36=0,解得n=  , ,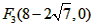 , ,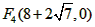 。 。 |
  |

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目

 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D. 如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根. (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是 如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.
如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC. 如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).