��Ŀ����
����Ŀ����ͼ����A��B�ڶ�������ĺ�����MN�ϣ����յ��Ѵ�����dz�Ĵ�P������źţ���֪��P�ڴ�A�ı�ƫ��60�㷽���ϣ��ڴ�B�ı�ƫ��37�㷽���ϣ�AP=30��� 
��1���߹���ͼ������P��AB����ֱ�ߵĴ��ߣ�����ΪE��Ҫ������ͼ�ۼ�����д��������
��2����P��������MN�ľ��루��PE�ij�����
��3������A����B�ֱ���20����/ʱ��15����/ʱ���ٶ�ͬʱ����������ֱ��ǰ����Ԯ����ͨ�������ж����Ҵ��ȵ��ﴬP�������ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��
���𰸡�
��1���⣺��ͼ��ʾ��
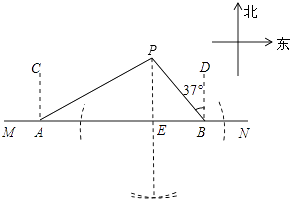
��2���⣺������ã���PAE=30�㣬AP=30���
��Rt��APE��PE=APsin��PAE=APsin30��=15����
��3���⣺��Rt��PBE�У�PE=15�����PBE=53�㣬
��BP= ![]() =
= ![]() ���
���
A����Ҫ��ʱ��Ϊ�� ![]() =1.5Сʱ��B����Ҫ��ʱ��Ϊ��
=1.5Сʱ��B����Ҫ��ʱ��Ϊ�� ![]() =1.25Сʱ��
=1.25Сʱ��
��1.5��1.25��
��B���ȵ���
����������1������ֱ�����ǰ���90���ֱ��ֱ�ӹ���P��AB����ֱ�ߵĴ����ɣ���2����Rt��APE���PE���ɣ���3����Rt��BPF�У����BP���ֱ��������Ҵ���Ҫ��ʱ�䣬���������жϣ�
�����㾫�����������⣬������Ҫ�˽���ڷ��������(ָ����ָ�Ϸ�������Ŀ�귽�� �����ɵ�С��90���ˮƽ�ǣ����������)��





