题目内容
【题目】如图,在平面直角坐标系内,已知点![]() 、点
、点![]() ,动点
,动点![]() 从点
从点![]() 开始在线段
开始在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动,同时动点
移动,同时动点![]() 从点
从点![]() 开始在线段
开始在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动,设点
移动,设点![]() 、
、![]() 移动的时间为
移动的时间为![]() 秒.
秒.
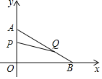
![]() 求点
求点![]() 的坐标;
的坐标;
![]() 当
当![]() 为何值时,
为何值时,![]() 的面积为
的面积为![]() 个平方单位?
个平方单位?
【答案】![]() ;(2)当
;(2)当![]() 为
为![]() 秒或
秒或![]() 秒时,
秒时,![]() 的面积为
的面积为![]() 个平方单位.
个平方单位.
【解析】
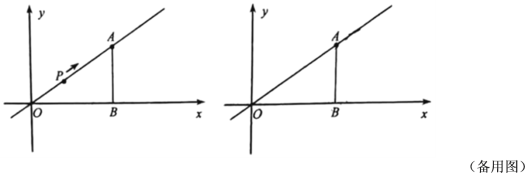
(1)过点Q作QH⊥AO于H,如图所示,易证△AHQ∽△AOB,根据相似三角形的性质可用t的代数式表示出QH,进而表示出HO的长,进而得出答案;
(2)利用(1)中所求,从而得到△APQ的面积与t的关系,根据条件就可求出t的值.
解:![]() 如图,
如图,
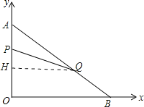
过点![]() 作
作![]() 于
于![]() ,如图所示,
,如图所示,
则有![]() .
.
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
故![]()
解得:![]() ,
,
则![]() ;
;
![]() 由
由![]() 得:
得:![]() .
.
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() .
.
∴当![]() 为
为![]() 秒或
秒或![]() 秒时,
秒时,![]() 的面积为
的面积为![]() 个平方单位.
个平方单位.

练习册系列答案
相关题目