题目内容
【题目】已知，在平行四边形
中，
，
为
边的中点，连接
；
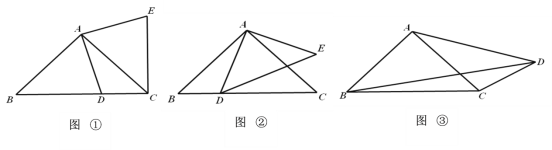
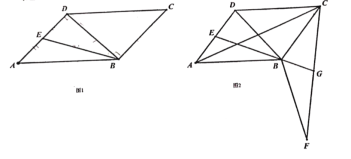
（1）如图1，若
，
，求平行四边形的面积；
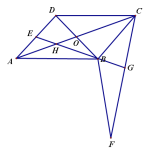
（2）如图2，连接
，将
沿
翻折得到
，延长
与
交于点
，求证：
.
【答案】（1）4（2）见解析
【解析】
（1）设DE=x,则BD=2x，根据勾股定理即可求解x,故可求解;
（2）根据题意先证明△ABE≌△DCO，再证明△DEB≌△GBC，即可得证.
（1）设DE=x,
∵
，
为
边的中点
∴BD=AD=2x,
在Rt△BED中，有(2x)2+x2=(
)2
解得x=1
∴AD=2=BD，
平行四边形
的面积=AD×BD=4；
（2）如图，设AC,BD交于O，AC,BE交于H点，
∵，为边的中点
∴AE=
AD=BC,DO=BD
∴AE=DO
∵AD=BD=BC,
∴
在△ABE和△DCO中
∴△ABE≌△DCO
∴
∵
∴
∵
∴
∵AD∥BC，
∴
又∵DB=BC，
∴△DEB≌△GBC
∴
即
练习册系列答案
相关题目
【题目】某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的，如果期末评价成绩80分以上（含80分），则评为“优秀”．下面表中是小张和小王两位同学的成绩记录：
完成作业 | 单元测试 | 期末考试 | |
小张 | 70 | 90 | 80 |
小王 | 60 | 75 |
（1）若按三项成绩的平均分记为期末评价成绩，请计算小张的期末评价成绩；
（2）若按完成作业、单元检测、期末考试三项成绩按
的权重来确定期末评价成绩．
①请计算小张的期末评价成绩为多少分？
②小王在期末（期末成绩为整数）应该最少考多少分才能达到优秀？
