题目内容
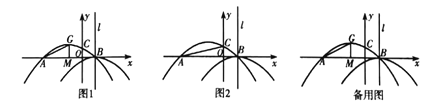
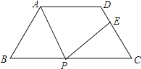
【题目】如图,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为下底
为下底![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,过点
,过点![]() 作射线
作射线![]() 交线段
交线段![]() 于点
于点![]() ,使得
,使得![]() ,若
,若![]() ,则
,则![]() ________.
________.
【答案】![]() 或
或![]()
【解析】
作AF⊥BC于F,∠B=60°,由等腰梯形的性质得到AF是BC、AD差的一半,在Rt△ABF中,根据∠B的度数及BF的长可求得AB的值,由DE:EC=5:3时,求出DE、CE的值.由等腰梯形的性质可得出∠B=∠C,根据三角形外角的性质可证得∠EPC=∠BAP,可证△ABP∽△PCE,设BP的长为x,进而可表示出PC的长,然后根据相似三角形,可得出关于AB、BP、PC、CE的比例关系式,求出BP的长.
如图,过A作AF⊥BC于F;
∵等腰梯形ABCD中,AD=6cm,BC=14cm,
∴BF=4
∵Rt△ABF中,∠B=60°,BF=4;
∴AB=CD=8cm,
∵DE:EC=5:3,
∴EC=3,
由∠APC为△ABP的外角得∠APC=∠B+∠BAP;
∵∠B=∠APE
∴∠EPC=∠BAP
∵∠B=∠C
∴△ABP∽△PCE,
∴![]() =
=![]() ,
,
设BP=x,则PC=14x,
∴![]() =
=![]() ,
,
解得:x1=2,x2=12,
∴BP的长为2或12.
故答案为:2或12.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目