题目内容
【题目】如图,等边△ABC和等腰Rt△DEF均内接于⊙O,∠D=Rt∠,EF∥AC,AC分别交DE,DF于点P,Q,EF分别交AB,BC于点G,H,则 ![]() 的值是( )
的值是( ) 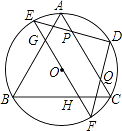
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:连接OD,OB,OD与AC交于K,
∵△DEF是等腰直角三角形,
∴OD⊥EF,
∵EF∥AC,
∴OD⊥AC,
∵等边△ABC内接于⊙O,
∴B,O,K,D四点共线,
∴OB=OD=2OK=2DK,
∵△ABC是等边三角形,GH∥AC,
∴△BHG是等边三角形,
∴∠BGO=60°,
∴BG=GH= ![]() =
= ![]() OB,
OB,
∵△DEF是等腰直角三角形,PQ∥EF,
∴△PDQ是等腰直角三角形,
∴PQ=2DK=OB,
∴ ![]() =
= ![]() =
= ![]() ,
,
故选C.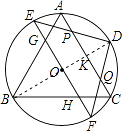
【考点精析】掌握三角形的外接圆与外心是解答本题的根本,需要知道过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目