题目内容
【题目】如图，在四边形ABCD中，∠D=∠BCD=90°，∠B=60°，AB=6，AD=9，点E是CD上的一个动点（E不与D重合），过点E作EF∥AC，交AD于点F（当E运动到C时，EF与AC重合），把△DEF沿着EF对折，点D的对应点是点G．设DE=x，△GEF与四边形ABCD重叠部分的面积为y．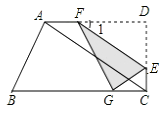
（1）求CD的长及∠1的度数；
（2）若点G恰好在BC上，求此时x的值；
（3）求y与x之间的函数关系式，并求x为何值时，y的值最大？最大值是多少？
【答案】
（1）
解：如图1，
过点A作AH⊥BC于点H，
∵在Rt△AHB中，AB=6，∠B=60°，
∴AH=ABsinB=6× 
=3 
，
∵∠D=∠BCD=90°，
∴四边形AHCD为矩形，
∴CD=AH=3 ，
∵ 
，
∴∠CAD=30°，
∵EF∥AC，
∴∠1=∠CAD=30°
（2）
解：若点G恰好在BC上，如图2，
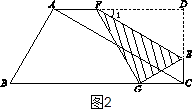
由对折的对称性可知Rt△FGE≌Rt△FDE，
∴GE=DE=x，∠FEG=∠FED=60°，
∴∠GEC=60°，
∵△CEG是直角三角形，
∴∠EGC=30°，
∴在Rt△CEG中，EC= 
EG= x，
由DE+EC=CD 得 
，
∴x=2
（3）
解：分两种情形：
第一种情形：当 
时，如图3，
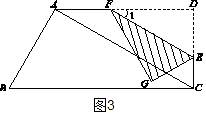
在Rt△DEF中，tan∠1=tan30°= 
，
∴DF=x÷ 
= x，
∴y=S△EGF=S△EDF= 
= 
= 
，
∵ ＞0，对称轴为y轴，
∴当 ，y随x的增大而增大，
∴当x=2 时，y最大值= × 
=6 ；
第二种情形：当2 ＜x≤3 时，如图4，
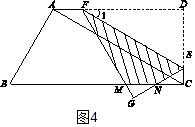
设FG，EG分别交BC于点M、N，
（法一）∵DE=x，
∴EC= 
，NE=2 
，
∴NG=GE﹣NE= 
= 
，
又∵∠MNG=∠ENC=30°，∠G=90°，
∴MG=NGtan30°= 
，
∴ 
= 
∴y=S△EGF﹣S△MNG= 
= 
∵ 
，对称轴为直线 
，
∴当2 ＜x≤3 时，y有最大值，且y随x的增大而增大，
∴当 
时， 
=9 ，
综合两种情形：由于6 ＜9 ；
∴当 时，y的值最大，y的最大值为9 ．
【解析】（1）如图1，作辅助线AH⊥BC，AH的长就是CD的长，根据直角三角形中的特殊三角函数值可以求AH的长，即CD=AH=3 ，在直角△ACD中，求∠CAD=30°，由平行线的同位角相等可以得∠1=∠CAD=30°；（2）如图2，由对折得：Rt△FGE≌Rt△FDE，则GE=DE=x，∠FEG=∠FED=60°，从而求得直角△GEC中，EC= x，根据DE+EC=CD 列式可求得x的值（3）分两种情形：
第一种情形：当 时，如图3，△GEF完全在四边形内部分，重叠部分面积就是△GEF的面积；
第二种情形：当2 ＜x≤3 时，如图4，重叠部分是△GEF的面积﹣△MNG的面积，所以要根据特殊的三角函数值求MG、NG的长，代入面积公式即可．
再根据两种情形的最大值作对比得出结果．
