题目内容
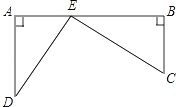
【题目】如图，铁路上A，B两点相距25km，C，D为两庄，DA⊥AB于A，CB⊥AB于B，已知DA=15km，CB=10km，现在要在铁路AB上建一个土特产品收购站E，使得C，D两村到E站的距离相等．问：
（1）在离A站多少km处？
（2）判定三角形DEC的形状．
【答案】（1）10km;(2) △DEC是直角三角形，理由见解析.
【解析】分析：（1）根据使得C，D两村到E站的距离相等，需要证明
，再根据
得出
（2）
的形状是直角三角形，利用
≌
，得出
，进而可以证明．
详解：(1)∵使得C，D两村到E站的距离相等.
∴DE=CE，
∵DA⊥AB于A，CB⊥AB于B，
∴
∴
∴
设AE=x,则BE=ABAE=(25x)，
∵DA=15km，CB=10km，
∴
解得：x=10，
∴AE=10km；
(2)△DEC是直角三角形，理由如下：
∵△DAE≌△EBC，
∴∠DEA=∠ECB，∠ADE=∠CEB，
∴
∴
即△DEC是直角三角形.
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
