题目内容
【题目】在平面直角坐标系xOy中，直线y=2x﹣3与y轴交于点A，点A与点B关于x轴对称，过点B作y轴的垂线l，直线l与直线y=2x﹣3交于点C．
（1）求点C的坐标；
（2）如果抛物线y=nx2﹣4nx+5n（n＞0）与线段BC有唯一公共点，求n的取值范围．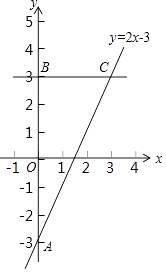 
【答案】
（1）解：∵直线y=2x﹣3与y轴交于点A（0，﹣3），
∴点A关于x轴的对称点B（0，3），l为直线y=3，
∵直线y=2x﹣3与直线l交于点C，
∴点C坐标为（3，3），
（2）解：∵抛物线y=nx2﹣4nx+5n（n＞0），
∴y=nx2﹣4nx+4n+n=n（x﹣2）2+n（n＞0）
∴抛物线的对称轴为直线x=2，顶点坐标为（2，n），
∵点B（0，3），点C（3，3），
①当n＞3时，抛物线的最小值为n＞3，与线段BC无公共点；
②当n=3时，抛物线的顶点为（2，3），在线段BC上，此时抛物线与线段BC有一个公共点；
③当0＜n＜3时，抛物线最小值为n，与线段BC有两个公共点；
如果抛物线y=n（x﹣2）2+n经过点B，则3=5n，解得n= 
，
由抛物线的对称轴为直线x=2，可知抛物线经过点（4，3），
点（4，3）不在线段BC上，此时抛物线与线段BC有一个公共点B；
如果抛物线y=n（x﹣2）2+n经过点C，则3=2n，解得n= 
，
由抛物线的对称轴为直线x=2，可知抛物线经过点（1，3），
点（1，3）在线段BC上，此时抛物线与线段BC有两个公共点；
综上所述，当 ≤n＜ 或n=3时，抛物线与线段BC有一个公共点．
【解析】（1）根据题意分别求出点A、B、C的坐标；（2）求得抛物线的对称轴，顶点的坐标；再分类讨论①当n＞3时；②当n=3时；③当0＜n＜3时，抛物线y=nx2﹣4nx+5n（n＞0）与线段BC有唯一公共点，求n的取值范围．
【考点精析】通过灵活运用一次函数的性质和二次函数的性质，掌握一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．
