题目内容
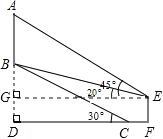
【题目】如图,AB是半圆O的直径,按以下步骤作图:
(1)分别以A,B为圆心,大于AO长为半径作弧,两弧交于点P,连接OP与半圆交于点C;
(2)分别以A,C为圆心,大于![]() AC长为半径作弧,两弧交于点Q,连接OQ与半圆交于点D;
AC长为半径作弧,两弧交于点Q,连接OQ与半圆交于点D;
(3)连接AD,BD,BC,BD与OC交于点 E.根据以上作图过程及所作图形,下列结论:①BD平分∠ABC;②BC∥OD;③CE=OE;④AD2=ODCE;所有正确结论的序号是( )
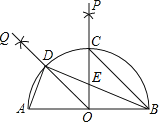
A.①②B.①④C.②③D.①②④
【答案】D
【解析】
由作图可知,OP垂直平分线段AB,OQ平分∠AOC,利用平行线的判定,相似三角形的性质一一判断即可.
解:由作图可知,OP垂直平分线段AB,OQ平分∠AOC,连接CD,
∴![]() ,
,
∴∠ABD=∠CBD,
即BD平分∠ABC,故①正确;
∵OP⊥AB,
∴∠AOC=∠BOC=90°,
∴∠AOD=![]() ∠AOC=45°,
∠AOC=45°,
∵OB=OC,
∴∠OBC=45°,
∴∠AOD=∠OBC=45°,
∴OD∥BC,故②正确;
由OD∥BC,
∴![]() =
=![]() <1,
<1,
∴OE<EC,故③错误;
∵∠DCE=∠DCO,∠CDE=∠COD=45°,
∴△DCE∽△OCD,
∴![]() =
=![]() ,
,
∴CD2=ODCE,
∵![]() ,
,
∴AD=CD,
∴AD2=ODCE,故④正确.
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目