题目内容
【题目】如图,在□ABCD中,对角线AC , BD相交于点O , E , F是对角线AC上的两点,当点E , F满足下列哪个条件时,四边形DEBF不一定是平行四边形( ) 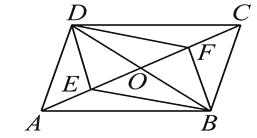
A.AE=CF
B.∠AED=∠CFB
C.∠ADE=∠CBF
D. DE=BF
【答案】D
【解析】A,∵AE=CF ,
∴OE=OF ,
∵DO=BO ,
∴四边形DEBF是平行四边形.
B,∵∠AED=∠CFB ,
∴∠DEO=∠BFO ,
∴△DOE ≌△BOF ,
∴EO=FO ,
∴四边形DEBF是平行四边形.
同理若∠ADE=∠CBF , 也能证明△DOE ≌△BOF , 从而四边形DEBF是平行四边形.只有答案D不能证明.
故选D.
【考点精析】根据题目的已知条件,利用平行四边形的判定的相关知识可以得到问题的答案,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目