题目内容
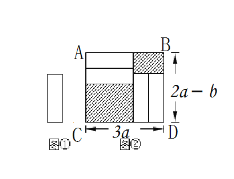
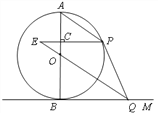
【题目】如图,矩形ABCD中,![]() ,
,![]() .点G,E分别在边AB,CD上,点F,H在对角线AC上.若四边形EFGH是菱形,则AG的长是( )
.点G,E分别在边AB,CD上,点F,H在对角线AC上.若四边形EFGH是菱形,则AG的长是( )

A.![]() B.5C.
B.5C.![]() D.6
D.6
【答案】B
【解析】
连接EG交AC于O,由矩形ABCD中,四边形EEFGH是菱形,易证得△CEO≌△AOG(AAS),即可得OA=OC,然后由勾股定理求得AC的长,继而求得OA的长,又由△AOG∽△ABC,利用相似三角形的对应边成比例,即可求得答案.
连接GE交AC于O,

∵四边形EFGH是菱形,
∴GE⊥AC,OG=OE,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CEO与△AOG中,
 ,
,
∴△CEO≌△AOG(AAS),
∴AO=CO,
∵AC=![]() ,
,
∴AO=![]() AC=2
AC=2![]() ,
,
∵∠CAB=∠CAB,∠AOG=∠B=90°,
∴△AOG∽△ABC,
∴![]() ,即
,即![]()
∴AG=5.
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
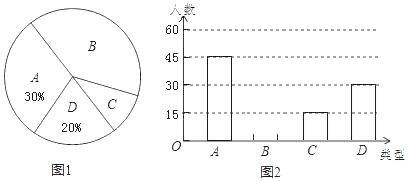
【题目】为了庆祝祖国70岁生日,阳光中学举行“向祖国70岁生日献礼”系列活动。学校团委为了组织好大型团体操表演,随机抽查部分七年级学生的身高,将学生身高分成四个组,并绘制成如下不完整的统计图表。
组别 | 身高 | 人数 |
1组 |
| 15 |
2组 |
|
|
3组 |
|
|
4组 |
| 10 |
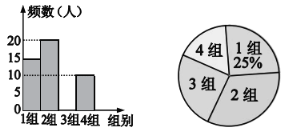
根据以上信息,解答下列问题:
(1)在统计表中,![]() 的值是________;本次调查的学生人数是________人.
的值是________;本次调查的学生人数是________人.
(2)补全频数分布直方图.
(3)在“祖国万岁”方队中,列队形成“祖国”二字学生的身高应该在![]() 的范围,该校七年级480名学生中,身高符合该条件的学生约有多少人?
的范围,该校七年级480名学生中,身高符合该条件的学生约有多少人?