��Ŀ����
����Ŀ���������龳�����ۺ�ʵ�����ϣ�ͬѧ������ͼ�ε�ƽ����Ϊ���չ��ѧ�����ͼ�٣��Ƚ�һ�ų�Ϊ4����Ϊ3�ľ���ֽƬ�ضԽ�������ƴ����ͼ��ʾ���ı���![]() ��
��![]() ��
��![]() ����ƴ�õ��ı���
����ƴ�õ��ı���![]() ���ܳ���_____.
���ܳ���_____.

���������֣���ͼ���е�![]() ��������
��������![]() ����ƽ�ƣ�����
����ƽ�ƣ�����![]() ��
��![]() ��
��![]() ��
��![]() ����ͼ��.��
����ͼ��.��![]() ��ƽ�ƾ�����
��ƽ�ƾ�����![]() �ij���ʱ�����ı���
�ij���ʱ�����ı���![]() ���ܳ�.
���ܳ�.
������̽������ͼ���е�![]() ������������
������������![]() ����ƽ�ƣ������������䣬���ı���
����ƽ�ƣ������������䣬���ı���![]() ������ʱ�����ı���
������ʱ�����ı���![]() �ضԽ��������õõ����ĸ�������ƴ�����������ȵľ��Σ�ֱ��д�����п���ƴ�ɵľ����ܳ�.
�ضԽ��������õõ����ĸ�������ƴ�����������ȵľ��Σ�ֱ��д�����п���ƴ�ɵľ����ܳ�.
���𰸡��������龳��16�����������֡�6+2![]() ��������̽����20��22��
��������̽����20��22��
��������
�������龳��
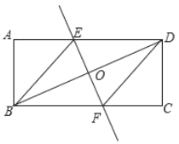
���������⣬�ɵ�AB=CD��AC=BD����ADB=��DBC=90����Ȼ����ݹ��ɶ������ɵ�AB����������ı���ABCD���ܳ���
���������֡�
������ƽ�ƣ���AE=CF=3��DE=BF���ٸ���ƽ�У������ж��ı���AECF��ƽ���ı��Σ�Ȼ����ݹ��ɶ������ɵ�AF����������ı���AECF���ܳ���
������̽����
������ƽ�ƣ��õ���E���F�غ�ʱ���ı���ABCDΪ���Σ��ó���Խ��ߵij����ضԽ���������������ɵľ����������������6Ϊ����4Ϊ���ľ��κ���3Ϊ����8Ϊ���ľ��Σ�����������ܳ�.
�����⣬�ɵ�AB=CD��AC=BD����ADB=��DBC=90��
����![]() ��
��![]() ��
��
����ݹ��ɶ������ɵ�![]()
���ı���![]() ���ܳ���
���ܳ���![]()
�ʴ�Ϊ16.
��ƽ�ƣ���AE=CF=3��DE=BF��
��AE��CF��
���ı���AECF��ƽ���ı��Σ�
��BE=DF=4��
��EF=DE=2��
��Rt��AEF����AEF=90����
�ɹ��ɶ�������AF=![]() =
=![]() ��
��
���ı���AECF���ܳ�Ϊ2AE+2AF=6+2![]() ��
��
��ƽ�ƣ��õ���E���F�غ�ʱ���ı���ABCDΪ���Σ�AE=CE=3��BE=DE=4���ضԽ���������������ɵľ��������������
����6Ϊ����4Ϊ���ľ��Σ����ܳ�Ϊ![]() ��
��
����3Ϊ����8Ϊ���ľ��Σ����ܳ�Ϊ![]() .
.
�ʴ�Ϊ20��22��