题目内容
【题目】已知:x为实数,[x]表示不超过x的最大整数,如[3.14]=3,[1]=1,[﹣1.2]=﹣2.请你在学习,理解上述定义的基础上,解决下列问题:设函数y=x﹣[x].
(1)当x=2.15时,求y=x﹣[x]的值;
(2)当0<x<2时,求函数y=x﹣[x]的表达式,并画出函数图象;
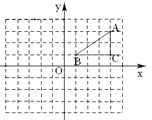
(3)当﹣2<x<2时,平面直角坐标系xOy中,以O为圆心,r为半径作圆,且r≤2,该圆与函数y=x﹣[x]恰有一个公共点,请直接写出r的取值范围.
【答案】(1)0.15;(2)①y=x,②当1y=x﹣1, (3)r的取值范围是:0<r<![]() 或x=
或x=![]() .
.
【解析】试题分析:(1)根据[x]的定义进行计算即可;
(2)由已知条件:0<x<1,1≤x<2进行分类讨论,由此可求出结论;
(3)把自变题x在-2<x<2内分四种情况得出相应的函数关系式,并画出图形,确定r的取值即可.
试题解析:解:(1)当x=2.15时,y=x﹣[x]=2.15﹣[2.15]=2.15﹣2=0.15;
(2)①当0<x<1时,[x]=0.∵y=x﹣[x],∴y=x;
②当1≤x<2时,[x]=1
∵y=x﹣[x],∴y=x﹣1;

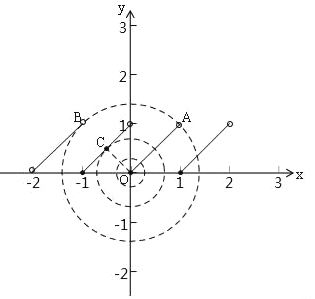
(3)函数y=x﹣[x](﹣2<x<2),如图,OA=![]() .
.
①当﹣2<x<﹣1,[x]=﹣2,y=x﹣[x]=x+2,②当﹣1≤x<0时,[x]=﹣1,y=x﹣[x]=x+1,③当0≤x<1时,[x]=0,y=x﹣[x ]=x,④当1≤x<2时,[x]=1,y=x﹣[x]=x﹣1,当r=OA= ![]() 时,⊙O与直线y=x﹣1相交于一点,OC=
时,⊙O与直线y=x﹣1相交于一点,OC= ![]() OA=
OA=![]() ,当0<r<
,当0<r<![]() 时,⊙O总与直线y=x相交于一点;
时,⊙O总与直线y=x相交于一点;
综上所述:r的取值范围是:0<r<![]() 或x=
或x= ![]() .
.

练习册系列答案
相关题目