题目内容
【题目】把四张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为3a厘米，宽为（2a－b）厘米）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示．
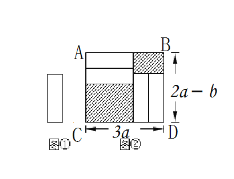
（1）求大长方形ABCD的周长；
（2）求图②中两块阴影部分周长之和．（用含a，b的式子表示）
【答案】(1)10a-2b;(2)8a-4b.
【解析】
(1)直接运用长方形周长公式进行求解即可；（2）设小长方形的长为m，宽为n，然后根据分别表示两块阴影部分的周长，再求和即可.
解：（1）大长方形ABCD的周长为：2（3a+2a-b）=10a-2b；
（2）设小长方形的长为m，宽为n；
则大阴影的长宽分别为：3a-2n，2a-b-2n，周长为：2（3a-2n+2a-b-2n）=10a-2b-8n
小阴影的长宽分别为：3a-m，2a-b-m，周长为：2（3a-m+2a-b-m）=10a-2b-4m
由图2可知：m+2n=3a
两块阴影部分周长之和2（10a-2b）-4m-8n=2（10a-2b）-4（m+2n）=20a-4b-12a=8a-4b
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
