题目内容
【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,且∠BON=55°,求∠BOD的度数. 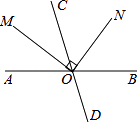
【答案】解:∵ON⊥OM, ∴∠MON=90°,
∵∠BON=55°,
∴∠AOM=180°﹣90°﹣55°=35°,
∵射线OM平分∠AOC,
∴∠AOC=2∠AOM=70°,
∴∠BOD=∠AOC=70°.
【解析】首先根据垂线的定义和已知条件求出∠AOM的度数,根据角平分线的定义求出∠AOC的度数,根据对顶角相等的性质即可得出所求.
【考点精析】根据题目的已知条件,利用角的平分线和对顶角和邻补角的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.

练习册系列答案
相关题目