题目内容
【题目】如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
(1)若∠C=38°,则∠ABD= ;
(2)求证:BC=AB+AD;
(3)求证:BC2=AB2+ABAC.

【答案】(1)33°;(2)证明见解析.(3)证明见解析.
【解析】试题分析:(1)在BC上截取BE=AB,利用“边角边”证明△ABD和△BED全等,根据全等三角形对应边相等可得DE=AD,全等三角形对应角相等可得∠AED=∠A,然后求出∠C=∠CDE,根据等角对等边可得CE=DE,然后结合图形整理即可得证;
(2)由(1)知:△ABD≌△BED,根据全等三角形对应边相等可得DE=AD,全等三角形对应角相等可得∠AED=∠A,然后求出∠C=∠CDE,根据等角对等边可得CE=DE,等量代换得到EC=AD,即得答案BC=BE+EC=AB+AD;
(3)为了把∠A=2∠C转化成两个角相等的条件,可以构造辅助线:在AC上取BF=BA,连接AE,根据线段的垂直平分线的性质以及三角形的内角和定理的推论能够证明AB=F.再根据勾股定理表示出BC2,AB2.再运用代数中的公式进行计算就可证明.
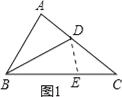
试题解析:(1)在BC上截取BE=BA,如图1,
在△ABD和△BED中,
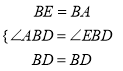 ,
,
∴△ABD≌△BED,
∴∠BED=∠A,
∵∠C=38°,∠A=2∠C,
∴∠A=76°,
∴∠ABC=180°﹣∠C﹣∠A=66°,
BD平分∠ABC,
∴∠ABD=33°;
(2)由(1)知:△ABD≌△BED,
∴BE=AB,DE=AD,∠BED=∠A,
又∵∠A=2∠C,
∴∠BED=∠C+∠EDC=2∠C,
∴∠EDC=∠C,
∴ED=EC,
∴EC=AD
∴BC=BE+EC=AB+AD;t
(3)如图2,过B作BG⊥AC于G,
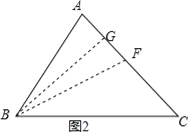
以B为圆心,BA长为半径画弧,交AC于F,
则BF=BA,
在Rt△ABG和Rt△GBG中,
![]() ,
,
∴Rt△ABG≌Rt△GBG,
∴AG=FG,
∴∠BFA=∠A,
∵∠A=2∠C,
∴∠BFA=∠FBC+∠C=2∠C,
∴∠FBC=∠C,
∴FB=FC,
FC=AB,
在Rt△ABG和Rt△BCG中,
BC2=BG2+CG2,
AB2=BG2+AG2
∴BC2﹣AB2=CG2﹣AG2=(CG+AG)(CG﹣AG)
=AC(CG﹣GF)=ACFC
=ACAB.

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案