题目内容
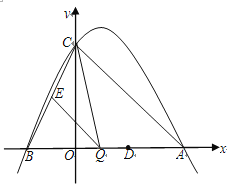
【题目】等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.

(1)求出S关于t的函数关系式;
(2)当点P运动几秒时,S△PCQ=S△ABC?
(3)作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.
【答案】(1)S=![]() (t<10),
(t<10),![]() (t>10); (2)
(t>10); (2)![]() ;(3)不变,理由参见解析.
;(3)不变,理由参见解析.
【解析】
试题由题可以看出P沿AB向右运动,Q沿BC向上运动,且速度都为1cm/s,S=![]() QC×PB,所以求出QC、PB与t的关系式就可得出S与t的关系,另外应注意P点的运动轨迹,它不仅在B点左侧运动,达到一定时间后会运动到右侧,所以一些问题可能会有两种可能出现的情况,这时我们应分类回答.
QC×PB,所以求出QC、PB与t的关系式就可得出S与t的关系,另外应注意P点的运动轨迹,它不仅在B点左侧运动,达到一定时间后会运动到右侧,所以一些问题可能会有两种可能出现的情况,这时我们应分类回答.
试题解析:(1)当t<10秒时,P在线段AB上,此时CQ=t,PB=10-t
∴s=![]() ×t×(10t)=
×t×(10t)=![]() (10tt2)
(10tt2)
当t>10秒时,P在线段AB得延长线上,此时CQ=t,PB=t-10
∴s=![]() ×t×(t10)=
×t×(t10)=![]() (t210t)
(t210t)
(2)∵S△ABC=![]() ABBC=50
ABBC=50
∴当t<10秒时,S△PCQ=![]() (10tt2)=50
(10tt2)=50
整理得t2-10t+100=0无解
当t>10秒时,S△PCQ=![]() (t210t)="50"
(t210t)="50"
整理得t2-10t-100=0解得x=5±5![]() (舍去负值)
(舍去负值)
∴当点P运动5+5![]() 秒时,S△PCQ=S△ABC.
秒时,S△PCQ=S△ABC.
(3)当点P、Q运动时,线段DE的长度不会改变
证明:过Q作QM⊥AC,交直线AC于点M
易证△APE≌△QCM,
∴AE=PE=CM=QM=![]() t,
t,
∴四边形PEQM是平行四边形,且DE是对角线EM的一半
又∵EM=AC=10![]()
∴DE=5![]()
∴当点P、Q运动时,线段DE的长度不会改变

 名师点拨卷系列答案
名师点拨卷系列答案【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 2 | 5 | 1 | 5 | 4 | 7 | 4 | 3 | 3 | 6 |
根据以上数据,解答下列问题:
(I)直接填空:第10次摸棋子摸到黑棋子的频率为 ;
(Ⅱ)试估算袋中的白棋子数量.