题目内容
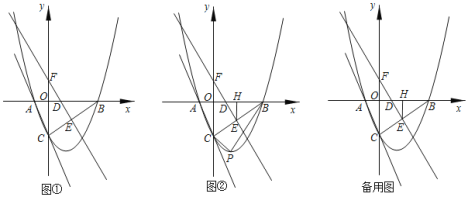
【题目】如图![]() ,在平面直角坐标系中,抛物线
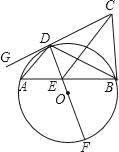
,在平面直角坐标系中,抛物线![]() 分别与x轴交于A,B两点,与y轴交于C点,直线EF垂直平分线段BC,分别交BC于点E,y轴于点F,交x轴于D.
分别与x轴交于A,B两点,与y轴交于C点,直线EF垂直平分线段BC,分别交BC于点E,y轴于点F,交x轴于D.
![]() 判定
判定![]() 的形状;
的形状;
![]() 在线段BC下方的抛物线上有一点P,当
在线段BC下方的抛物线上有一点P,当![]() 面积最大时,求点P的坐标及
面积最大时,求点P的坐标及![]() 面积的最大值;
面积的最大值;
![]() 如图
如图![]() ,过点E作
,过点E作![]() 轴于点H,将
轴于点H,将![]() 绕点E逆时针旋转一个角度
绕点E逆时针旋转一个角度![]() ,
,![]() 的两边分别交线段BO,CO于点T,点K,当
的两边分别交线段BO,CO于点T,点K,当![]() 为等腰三角形时,求此时KT的值.
为等腰三角形时,求此时KT的值.
【答案】![]() △ABC为直角三角形;
△ABC为直角三角形;![]() 当
当![]() 时,
时,![]() 面积最大,最大面积为
面积最大,最大面积为![]() ,此时
,此时![]() ;
;![]() 当
当![]() 是等腰三角形时,KT的值为
是等腰三角形时,KT的值为![]() 或
或![]() .
.
【解析】
(1)结论:△ABC是直角三角形.求出A、B、C三点坐标,求出AC、BC、AB的长,利用勾股定理的逆定理证明即可.
(2)作P作PG∥y轴,交BC于G,先利用待定系数法求直线BC的解析式为:![]() ,设P(x,
,设P(x,![]() ),则G(x,
),则G(x,![]() ),根据三角形面积公式表示△BCP面积,配方可得结论;
),根据三角形面积公式表示△BCP面积,配方可得结论;
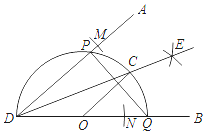
(3)①如图,当K与O重合,T与D重合时,△EKT的等腰三角形,求出KT即可解决问题.②如图,当TE=KE时,作KN⊥CE于N,EQ⊥OC于Q,则四边形OQEH是矩形,由△KEN≌△ETH,推出KN=EH=1,再想办法求出OK,OT即可解决问题.
![]() 为直角三角形,理由如下:
为直角三角形,理由如下:
当![]() 时,
时,![]() ,
,
![]() 点C的坐标为
点C的坐标为![]() ;
;
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 点A的坐标为
点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]() 为直角三角形.
为直角三角形.
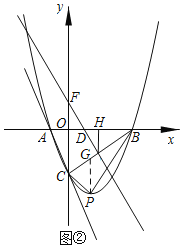
![]() 如图
如图![]() ,过P作
,过P作![]() 轴,交BC于G,
轴,交BC于G,
![]() 点B的坐标为
点B的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ,
,
易得直线BC的解析式为:![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]() 是直线BC下方抛物线上的点,
是直线BC下方抛物线上的点,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 面积最大,最大面积为
面积最大,最大面积为![]() ,此时
,此时![]() ;
;
![]() 如下图中,
如下图中,
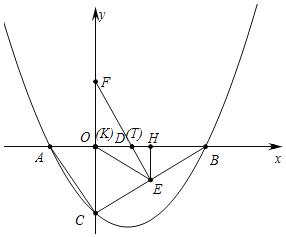
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
当K与O重合,T与D重合时,![]() 是等腰三角形,
是等腰三角形,
易知![]() ,
,
![]() ,
,
![]() .
.
![]() 如图,当
如图,当![]() 时,作
时,作![]() 于N,
于N,![]() 于Q,则四边形OQEH是矩形,
于Q,则四边形OQEH是矩形,
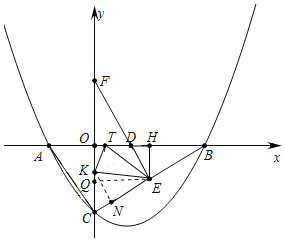
易知:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]() 中,易知
中,易知![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
综上所述,当![]() 是等腰三角形时,KT的值为
是等腰三角形时,KT的值为![]() 或
或![]() .
.