��Ŀ����
����Ŀ����ͼ����֪���κ���y=ax2+bx+3��a��0����ͼ����A��3��0����B��4��1��������y�ύ�ڵ�C������AB��AC��BC��
��1����˶��κ����Ĺ�ϵʽ��
��2���жϡ�ABC����״������ABC�����Բ��Ϊ��M����ֱ��д��Բ��M�����ꣻ
��3������������������BA����ƽ�ƣ�ƽ�ƺ��A��B��C�Ķ�Ӧ��ֱ��Ϊ��A1��B1��C1 �� ��A1B1C1�����Բ��Ϊ��M1 �� �Ƿ����ij��λ�ã�ʹ��M1����ԭ�㣿�����ڣ������ʱ�����ߵĹ�ϵʽ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�ѵ�A��3��0����B��4��1������y=ax2+bx+3�У�
![]() ��
��
��ã�  ��
��
������������ϵʽΪ��y= ![]() x2��
x2�� ![]() x+3��
x+3��
��2��
�⣺��ABC��ֱ�������Σ�
����B��BD��x���ڵ�D��
��֪��C����Ϊ����0��3��������OA=OC��
���ԡ�OAC=45�㣬
�֡ߵ�B����Ϊ����4��1����
��AD=BD��
���OAC=45�㣬
���BAC=180�㩁45�㩁45��=90�㣬
���ABC��ֱ�������Σ�
Բ��M������Ϊ����2��2����
��3��
�⣺����
ȡBC���е�M������M��ME��y���ڵ�E��
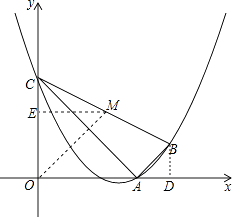
��M����������2��2����
��MC= ![]() =
= ![]() ��OM=2
��OM=2 ![]() ��
��
���MOA=45�㣬
�֡ߡ�BAD=45�㣬
��OM��AB��
��Ҫʹ������������BA����ƽ�ƣ���ʹ��M1����ԭ�㣬
��ƽ�Ƶij���Ϊ��2 ![]() ��
�� ![]() ��2
��2 ![]() +
+ ![]() ��
��
�ߡ�BAD=45�㣬
�������ߵĶ����������¾��ֱ�ƽ�� ![]() =
= ![]() �������
�������
�� ![]() =
= ![]() ����λ���ȣ�
����λ���ȣ�
��y= ![]() x2��
x2�� ![]() x+3=
x+3= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
��ƽ�ƺ������ߵĹ�ϵʽΪ��y= ![]() ��x��
��x�� ![]() +
+ ![]() ��2��
��2�� ![]() ��
�� ![]() ��
��
��y= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
��y= ![]() ��x��
��x�� ![]() +
+ ![]() ��2��
��2�� ![]() ��
�� ![]() ��
��
��y= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
��������������һ��λ�ã�ʹ��M1����ԭ�㣬��ʱ�����ߵĹ�ϵʽΪ��
y= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��y=
��y= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
����������1��ֱ�����ô���ϵ�������a��b��ֵ�����ó��𰸣���2�����ȵó���OAC=45�㣬�����ó�AD=BD�������OAC=45�㣬���ɵó��𰸣���3������������֪�ó�ԲMƽ�Ƶij���Ϊ��2 ![]() ��
�� ![]() ��2
��2 ![]() +
+ ![]() �������ó������ߵ�ƽ�ƹ��ɣ����ɵó��𰸣�
�������ó������ߵ�ƽ�ƹ��ɣ����ɵó��𰸣�