Question

【题目】已知抛物线y＝x2+bx+c经过点A（3﹣m，4），且过点B（3+m，4），A在B的左侧，顶点为P．

（1）求b的值；

（2）当c＝4时，求sin∠APB；

（3）抛物线y＝x2+bx+c上是否存在点Q，使得四边形OPQA是平行四边形？若存在，请求出点Q的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）b＝﹣6；（2）；（3）存在点Q的坐标分别是（5，7）或（1，﹣17），使得四边形OPQA是平行四边形

【解析】

（1）求出抛物线的对称轴方程为x＝3，则b的值可求出；

（2）过点B作BM⊥AP于点M，求出点P，A，B的坐标，求出AP长，根据三角形PAB的面积可求出BM长，则可求出sin∠APB；

（3）由题意得出点A的坐标为（3﹣m，4），点P的坐标为（3，4﹣m2），由平行四边形的性质可得点Q的坐标为Q（3+3﹣m，4﹣m2+4），代入抛物线解析式可求出m的值，则点Q的坐标可求出．

解：（1）由抛物线的对称性可知，对称轴是直线x＝，

又∵对称轴是直线x＝﹣，

∴b＝﹣6；

（2）当c＝4时，由（1）得到抛物线的表达式为y＝x2﹣6x+4＝（x﹣3）2﹣5，

∴点P的坐标为（3，﹣5）．

由x2﹣6x+4＝4得x1＝0，x2＝6，

∴点A，B的坐标分别为（0，4），（6，4），

如图，AB与抛物线的对称轴交于点N，过点B作BM⊥AP于点M，

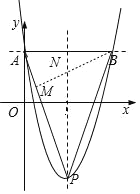
∴PN＝5+4＝9，AB＝6，＝3，

∵＝，

∴＝＝，

∴sin∠APB＝＝；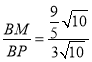

（3）存在点Q，使得四边形OPQA是平行四边形．理由是：

由（1）得抛物线为y＝x2﹣6x+c，点A的坐标为（3﹣m，4），

求得c＝13﹣m2，

∴点P的坐标为（3，4﹣m2），

∴抛物线的表达式为y＝x2﹣6x+c＝x2﹣6x+13﹣m2，

将线段OA平移，使点O与点P重合，得到线段PQ，

此时四边形OPQA是平行四边形．

由平移的性质可得，点Q的坐标为Q（3+3﹣m，4﹣m2+4），

即Q（6﹣m，8﹣m2），

若点Q在抛物线上，

有8﹣m2＝（6﹣m）2﹣6（6﹣m）+13﹣m2．

解得m1＝1，m2＝5，

当m1＝1时，点Q（5，7），

当m2＝5时，点Q（1，﹣17）．

综合以上可得，存在点Q的坐标分别是（5，7）或（1，﹣17），使得四边形OPQA是平行四边形．