��Ŀ����
����Ŀ����ͼ����֪��ABC�У���B=��C��AB=16���ף�BC=12���ף���DΪAB���е㣮�����P���߶�BC����ÿ��4�����ٶ���B����C���˶���ͬʱ����Q���߶�CA����ÿ��a�����ٶ���C����A���˶������˶�ʱ��Ϊt���룩��0��t��3����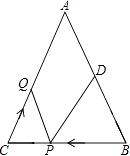
��1���õĴ���ʽ��ʾPC�ij��ȣ�
��2������P��Q���˶��ٶ���ȣ�����1���BPD���CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��3������P��Q���˶��ٶȲ���ȣ�����Q���˶��ٶ�aΪ����ʱ���ܹ�ʹ��BPD���CQPȫ�ȣ�
���𰸡�
��1��
�⣺PC=BC��PB=12��4t
��2��
�⣺����1���BPD���CQPȫ�ȣ�
��AB=16����DΪAB���е㣬
��BD=8��
����1���BP=CQ=4��
��BC=12��BP=4��
��CP=8��
��CP=BD��
�ڡ�BPD�͡�CQP�У�
 ��
��
���BPD�ա�CQP
��3��
�⣺��P��Q���˶��ٶȲ����ʱ����BPD���CQPȫ�ȣ���CP=BP��
��t= ![]() =
= ![]() �룬
�룬
��AB=16����DΪAB���е㣬
��BD=8��
��CQ=8��
���Q���˶��ٶ�a=8�� ![]() =
= ![]() ��
��
�൱��Q���˶��ٶ�aΪ ![]() ����/��ʱ����BPD���CQPȫ��
����/��ʱ����BPD���CQPȫ��
����������1���������⡢���ͼ�ν�𣻣�2���ֱ����BP��CQ�ij�������ȫ�������ε��ж�������𣻣�3������ȫ�������ε����������BPD���CQPȫ��ʱCQ�ij��������ٶȹ�ʽ���㼴�ɣ�

 �ο�������ϵ�д�
�ο�������ϵ�д� ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д�