题目内容
【题目】已知:如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AF⊥BE于点F,那么线段BE,CE,AF三者之间的数量关系是 . 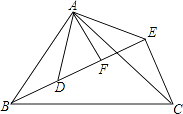
【答案】BE=CE+2AF
【解析】解:∵△ACB和△DAE均为等腰直角三角形, ∴AB=AC,AD=AE,∠BAC=∠DAE=90°,∠ADE=∠AED=45°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中, ,
,
∴△ABD≌△ACE,
∴BD=CE,∠ADB=∠AEC,
∵点A,D,E在同一直线上,
∴∠ADB=180﹣45=135°,
∴∠AEC=135°,
∴∠BEC=∠AEC﹣∠AED=135﹣45=90°;
∵∠DAE=90°,AD=AE,AF⊥DE,
∴AF=DF=EF,
∴DE=DF+EF=2AF,
∴BE=BD+DE=CE+2AF.
所以答案是:BE=CE+2AF.
【考点精析】通过灵活运用等腰直角三角形,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°即可以解答此题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目