题目内容
【题目】已知：如图，⊙O的直径AB与弦AC的夹角∠A=30°，AC=CP．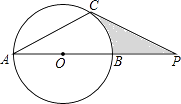
（1）求证：CP是⊙O的切线；
（2）若PC=6，AB=4 
，求图中阴影部分的面积．
【答案】
（1）解：如图，连接OC；
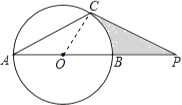
∵OA=OC，AC=CP，
∴∠A=∠OCA=30°，∠P=∠A=30°，
∴∠POC=∠A+∠OCA=60°，
∴∠OCP=180°﹣60°﹣30°=90°，
∴CP是⊙O的切线．
（2）解：∵AB=4 
，
∴OC=OB=2 ，
∴ 
= 
× 
=6 ，
=2π，
∴图中阴影部分的面积=6 ﹣2π．
【解析】（1）连接OC；由等边对等角得出∠A=∠OCA=30°，∠P=∠A=30°，利用三角形的外角得出∠POC=∠A+∠OCA=60°，进而根据三角形的内角和得出∠OCP=180°﹣60°﹣30°=90°，从而得出结论；（2）由三角形的面积公式得出S △ O C P = O C P C，由扇形面积公式得出S扇形OBC=2π，图中阴影部分的面积=S △ O C P-S扇形OBC计算即可。
【考点精析】掌握切线的判定定理和扇形面积计算公式是解答本题的根本，需要知道切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．
【题目】某石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表，请你解答下列问题：
出厂价 | 成本价 | 排污处理费 | |
甲种塑料 | 2100（元/吨） | 800（元/吨） | 200（元/吨） |
乙种塑料 | 2400（元/吨） | 1100（元/吨） | 100（元/吨） 另每月还需支付设备管理、维护费20000元 |
（1）设该车间每月生产甲、乙两种塑料各x吨，利润分别为y1元和y2元，分别求出y1和y2与x的函数关系式(注：利润=总收入-总支出)；
（2）已知该车间每月生产甲、乙两种塑料均不超过400吨，若某月要生产甲、乙两种塑料共700吨，求该月生产甲、乙塑料各多少吨时，获得的总利润最大？最大利润是多少？
