题目内容
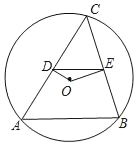
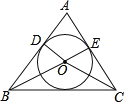
【题目】如图，⊙O是△ABC的内切圆，切AB，AC于点D、E，∠DOE＝110°，则∠BOC的度数为（ ）
A.115°B.120°C.125°D.135°
【答案】C
【解析】
根据内切圆的性质可得AD⊥OD，AC⊥OE，再求得∠A＝360°﹣2×90°﹣110°＝70°，然后利用角平分线的性质求出∠BOC＝125°.
解：∵⊙O是△ABC的内切圆，切AB，AC于点D、E，
∴AD⊥OD，AC⊥OE，
∴∠ADO＝∠AEO＝90°，
∵∠DOE＝110°，
∴∠A＝360°﹣2×90°﹣110°＝70°，
∴∠ABC+∠ACB＝180°﹣70°＝110°，
∵O为△ABC内心，
∴∠OBC＝
∠ABC，∠OCB＝∠ACB，
∴∠OBC+∠OCB＝55°，
∴∠BOC＝180°﹣55°＝125°，
故选：C．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
