Question

【题目】在△ABC中，BC=AC，∠BCA=90°，P为直线AC上一点，过点A作AD⊥BP于点D，交直线BC于点Q．

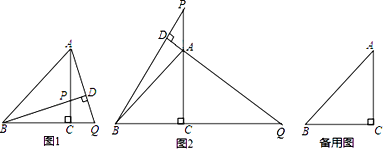
（1）如图1，当P在线段AC上时，求证：BP=AQ；

（2）如图2，当P在线段CA的延长线上时，（1）中的结论是否成立？________（填“成立”或“不成立”）

（3）在（2）的条件下，当∠DBA=________时，存在AQ=2BD，说明理由．

Answer 1

【答案】（1）详见解析；（2）成立； （3）22.5°，理由详见解析.

【解析】试题分析：（1）首先根据内角和定理得出∠DAP=∠CBP，进而得出

△ACQ≌△BCP即可得出答案；
（2）延长BA交PQ于H，由于 得到 推出△AQC≌△BPC(ASA)，即可得出结论；
（3）当时，存在根据等腰三角形的性质得到BP=2BD，通过△PBC≌△ACQ，根据全等三角形的性质即可得到结论．

试题解析：

（1）证明：∵∠ACB=∠ADB=90°，∠APD=∠BPC，

∴∠DAP=∠CBP，

在△ACQ和△BCP中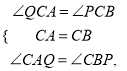

∴△ACQ≌△BCP（ASA），

∴BP=AQ

(2)成立，

理由：延长BA交PQ于H，

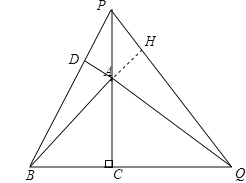
∠AQC=∠BQD,

∴∠CAQ=∠DBQ，

在△AQC和△BPC中,

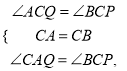
∴△AQC≌△BPC(ASA)，

∴AQ=BP，

故答案为：成立；

（3）22.5°，

当∠DBA=22.5°时，存在AQ=2BD，

理由：∵∠BAC=∠DBA+∠APB=45°，

∴∠PBA=∠APB=22.5°，

∴AP=AB，

∵AD⊥BP，

∴BP=2BD，

在△PBC与△QAC中，

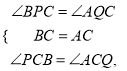
∴△PBC≌△ACQ，

∴AQ=PB，

∴AQ=2BD．

故答案为：22.5°.